给定一棵二叉树,求其最小深度。最小深度是从根节点到最近叶节点的最短路径上的节点数。
null
例如,二叉树下方的最小高度为2。
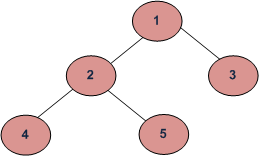
请注意,路径必须在叶节点上结束。例如,二叉树下方的最小高度也是2。
10 / 5
其思想是遍历给定的二叉树。对于每个节点,检查它是否是叶节点。如果是,则返回1。如果不是叶节点,则如果左子树为空,则右子树重复出现。如果右子树为空,则左子树重复出现。如果左子树和右子树都不为空,则取两个高度中的最小值。
下面是上述想法的实现。
C++
// C++ program to find minimum depth of a given Binary Tree #include<bits/stdc++.h> using namespace std; // A BT Node struct Node { int data; struct Node* left, *right; }; int minDepth(Node *root) { // Corner case. Should never be hit unless the code is // called on root = NULL if (root == NULL) return 0; // Base case : Leaf Node. This accounts for height = 1. if (root->left == NULL && root->right == NULL) return 1; int l = INT_MAX, r = INT_MAX; // If left subtree is not NULL, recur for left subtree if (root->left) l = minDepth(root->left); // If right subtree is not NULL, recur for right subtree if (root->right) r = minDepth(root->right); //height will be minimum of left and right height +1 return min(l , r) + 1; } // Utility function to create new Node Node *newNode( int data) { Node *temp = new Node; temp->data = data; temp->left = temp->right = NULL; return (temp); } // Driver program int main() { // Let us construct the Tree shown in the above figure Node *root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); cout << "The minimum depth of binary tree is : " << minDepth(root); return 0; } |
JAVA
/* Java implementation to find minimum depth of a given Binary tree */ /* Class containing left and right child of current node and key value*/ class Node { int data; Node left, right; public Node( int item) { data = item; left = right = null ; } } public class BinaryTree { //Root of the Binary Tree Node root; int minimumDepth() { return minimumDepth(root); } /* Function to calculate the minimum depth of the tree */ int minimumDepth(Node root) { // Corner case. Should never be hit unless the code is // called on root = NULL if (root == null ) return 0 ; // Base case : Leaf Node. This accounts for height = 1. if (root.left == null && root.right == null ) return 1 ; // If left subtree is NULL, recur for right subtree if (root.left == null ) return minimumDepth(root.right) + 1 ; // If right subtree is NULL, recur for left subtree if (root.right == null ) return minimumDepth(root.left) + 1 ; return Math.min(minimumDepth(root.left), minimumDepth(root.right)) + 1 ; } /* Driver program to test above functions */ public static void main(String args[]) { BinaryTree tree = new BinaryTree(); tree.root = new Node( 1 ); tree.root.left = new Node( 2 ); tree.root.right = new Node( 3 ); tree.root.left.left = new Node( 4 ); tree.root.left.right = new Node( 5 ); System.out.println( "The minimum depth of " + "binary tree is : " + tree.minimumDepth()); } } |
Python3
# Python program to find minimum depth of a given Binary Tree # Tree node class Node: def __init__( self , key): self .data = key self .left = None self .right = None def minDepth(root): # Corner Case.Should never be hit unless the code is # called on root = NULL if root is None : return 0 # Base Case : Leaf node.This accounts for height = 1 if root.left is None and root.right is None : return 1 # If left subtree is Null, recur for right subtree if root.left is None : return minDepth(root.right) + 1 # If right subtree is Null , recur for left subtree if root.right is None : return minDepth(root.left) + 1 return min (minDepth(root.left), minDepth(root.right)) + 1 # Driver Program root = Node( 1 ) root.left = Node( 2 ) root.right = Node( 3 ) root.left.left = Node( 4 ) root.left.right = Node( 5 ) print (minDepth(root)) # This code is contributed by Nikhil Kumar Singh(nickzuck_007) |
C#
using System; /* C# implementation to find minimum depth of a given Binary tree */ /* Class containing left and right child of current node and key value*/ public class Node { public int data; public Node left, right; public Node( int item) { data = item; left = right = null ; } } public class BinaryTree { //Root of the Binary Tree public Node root; public virtual int minimumDepth() { return minimumDepth(root); } /* Function to calculate the minimum depth of the tree */ public virtual int minimumDepth(Node root) { // Corner case. Should never be hit unless the code is // called on root = NULL if (root == null ) { return 0; } // Base case : Leaf Node. This accounts for height = 1. if (root.left == null && root.right == null ) { return 1; } // If left subtree is NULL, recur for right subtree if (root.left == null ) { return minimumDepth(root.right) + 1; } // If right subtree is NULL, recur for left subtree if (root.right == null ) { return minimumDepth(root.left) + 1; } return Math.Min(minimumDepth(root.left), minimumDepth(root.right)) + 1; } /* Driver program to test above functions */ public static void Main( string [] args) { BinaryTree tree = new BinaryTree(); tree.root = new Node(1); tree.root.left = new Node(2); tree.root.right = new Node(3); tree.root.left.left = new Node(4); tree.root.left.right = new Node(5); Console.WriteLine( "The minimum depth of binary tree is : " + tree.minimumDepth()); } } // This code is contributed by Shrikant13 |
Javascript
<script> /* javascript implementation to find minimum depth of a given Binary tree */ /* Class containing left and right child of current node and key value*/ class Node { constructor(item) { this .data = item; this .left = this .right = null ; } } // Root of the Binary Tree let root; function minimumDepth() { return minimumDepth(root); } /* Function to calculate the minimum depth of the tree */ function minimumDepth( root) { // Corner case. Should never be hit unless the code is // called on root = NULL if (root == null ) return 0; // Base case : Leaf Node. This accounts for height = 1. if (root.left == null && root.right == null ) return 1; // If left subtree is NULL, recur for right subtree if (root.left == null ) return minimumDepth(root.right) + 1; // If right subtree is NULL, recur for left subtree if (root.right == null ) return minimumDepth(root.left) + 1; return Math.min(minimumDepth(root.left), minimumDepth(root.right)) + 1; } /* Driver program to test above functions */ root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); document.write( "The minimum depth of " + "binary tree is : " + minimumDepth(root)); // This code contributed by aashish1995 </script> |
输出:
The minimum depth of binary tree is : 2
上述解的时间复杂度为O(n),因为它只遍历树一次。 感谢Gaurav Ahirwar提供上述解决方案。
即使在最上面的叶子接近根的情况下,上述方法也可能最终完成二叉树的遍历。A. 更好的解决方案 就是进行水平顺序遍历。执行遍历时,返回遇到的第一个叶节点的深度。
下面是这个解决方案的实现。
C++
// C++ program to find minimum depth of a given Binary Tree #include<bits/stdc++.h> using namespace std; // A Binary Tree Node struct Node { int data; struct Node *left, *right; }; // A queue item (Stores pointer to node and an integer) struct qItem { Node *node; int depth; }; // Iterative method to find minimum depth of Binary Tree int minDepth(Node *root) { // Corner Case if (root == NULL) return 0; // Create an empty queue for level order traversal queue<qItem> q; // Enqueue Root and initialize depth as 1 qItem qi = {root, 1}; q.push(qi); // Do level order traversal while (q.empty() == false ) { // Remove the front queue item qi = q.front(); q.pop(); // Get details of the remove item Node *node = qi.node; int depth = qi.depth; // If this is the first leaf node seen so far // Then return its depth as answer if (node->left == NULL && node->right == NULL) return depth; // If left subtree is not NULL, add it to queue if (node->left != NULL) { qi.node = node->left; qi.depth = depth + 1; q.push(qi); } // If right subtree is not NULL, add it to queue if (node->right != NULL) { qi.node = node->right; qi.depth = depth+1; q.push(qi); } } return 0; } // Utility function to create a new tree Node Node* newNode( int data) { Node *temp = new Node; temp->data = data; temp->left = temp->right = NULL; return temp; } // Driver program to test above functions int main() { // Let us create binary tree shown in above diagram Node *root = newNode(1); root->left = newNode(2); root->right = newNode(3); root->left->left = newNode(4); root->left->right = newNode(5); cout << minDepth(root); return 0; } |
JAVA
// Java program to find minimum depth // of a given Binary Tree import java.util.*; class GFG { // A binary Tree node static class Node { int data; Node left, right; } // A queue item (Stores pointer to // node and an integer) static class qItem { Node node; int depth; public qItem(Node node, int depth) { this .node = node; this .depth = depth; } } // Iterative method to find // minimum depth of Binary Tree static int minDepth(Node root) { // Corner Case if (root == null ) return 0 ; // Create an empty queue for level order traversal Queue<qItem> q = new LinkedList<>(); // Enqueue Root and initialize depth as 1 qItem qi = new qItem(root, 1 ); q.add(qi); // Do level order traversal while (q.isEmpty() == false ) { // Remove the front queue item qi = q.peek(); q.remove(); // Get details of the remove item Node node = qi.node; int depth = qi.depth; // If this is the first leaf node seen so far // Then return its depth as answer if (node.left == null && node.right == null ) return depth; // If left subtree is not null, // add it to queue if (node.left != null ) { qi.node = node.left; qi.depth = depth + 1 ; q.add(qi); } // If right subtree is not null, // add it to queue if (node.right != null ) { qi.node = node.right; qi.depth = depth + 1 ; q.add(qi); } } return 0 ; } // Utility function to create a new tree Node static Node newNode( int data) { Node temp = new Node(); temp.data = data; temp.left = temp.right = null ; return temp; } // Driver Code public static void main(String[] args) { // Let us create binary tree shown in above diagram Node root = newNode( 1 ); root.left = newNode( 2 ); root.right = newNode( 3 ); root.left.left = newNode( 4 ); root.left.right = newNode( 5 ); System.out.println(minDepth(root)); } } // This code is contributed by 29AjayKumar |
Python3
# Python program to find minimum depth of a given Binary Tree # A Binary Tree node class Node: # Utility to create new node def __init__( self , data): self .data = data self .left = None self .right = None def minDepth(root): # Corner Case if root is None : return 0 # Create an empty queue for level order traversal q = [] # Enqueue root and initialize depth as 1 q.append({ 'node' : root , 'depth' : 1 }) # Do level order traversal while ( len (q)> 0 ): # Remove the front queue item queueItem = q.pop( 0 ) # Get details of the removed item node = queueItem[ 'node' ] depth = queueItem[ 'depth' ] # If this is the first leaf node seen so far # then return its depth as answer if node.left is None and node.right is None : return depth # If left subtree is not None, add it to queue if node.left is not None : q.append({ 'node' : node.left , 'depth' : depth + 1 }) # if right subtree is not None, add it to queue if node.right is not None : q.append({ 'node' : node.right , 'depth' : depth + 1 }) # Driver program to test above function # Lets construct a binary tree shown in above diagram root = Node( 1 ) root.left = Node( 2 ) root.right = Node( 3 ) root.left.left = Node( 4 ) root.left.right = Node( 5 ) print (minDepth(root)) # This code is contributed by Nikhil Kumar Singh(nickzuck_007) |
C#
// C# program to find minimum depth // of a given Binary Tree using System; using System.Collections.Generic; class GFG { // A binary Tree node public class Node { public int data; public Node left, right; } // A queue item (Stores pointer to // node and an integer) public class qItem { public Node node; public int depth; public qItem(Node node, int depth) { this .node = node; this .depth = depth; } } // Iterative method to find // minimum depth of Binary Tree static int minDepth(Node root) { // Corner Case if (root == null ) return 0; // Create an empty queue for // level order traversal Queue<qItem> q = new Queue<qItem>(); // Enqueue Root and initialize depth as 1 qItem qi = new qItem(root, 1); q.Enqueue(qi); // Do level order traversal while (q.Count != 0) { // Remove the front queue item qi = q.Peek(); q.Dequeue(); // Get details of the remove item Node node = qi.node; int depth = qi.depth; // If this is the first leaf node // seen so far. // Then return its depth as answer if (node.left == null && node.right == null ) return depth; // If left subtree is not null, // add it to queue if (node.left != null ) { qi.node = node.left; qi.depth = depth + 1; q.Enqueue(qi); } // If right subtree is not null, // add it to queue if (node.right != null ) { qi.node = node.right; qi.depth = depth + 1; q.Enqueue(qi); } } return 0; } // Utility function to create a new tree Node static Node newNode( int data) { Node temp = new Node(); temp.data = data; temp.left = temp.right = null ; return temp; } // Driver Code public static void Main(String[] args) { // Let us create binary tree // shown in above diagram Node root = newNode(1); root.left = newNode(2); root.right = newNode(3); root.left.left = newNode(4); root.left.right = newNode(5); Console.WriteLine(minDepth(root)); } } // This code is contributed by PrinciRaj1992 |
Javascript
<script> // Javascript program to find minimum depth // of a given Binary Tree class Node { // Utility function to create a new tree Node constructor(data) { this .data = data; this .left = this .right = null ; } } class qItem { constructor(node,depth) { this .node = node; this .depth = depth; } } function minDepth(root) { // Corner Case if (root == null ) return 0; // Create an empty queue for // level order traversal let q = []; // Enqueue Root and initialize depth as 1 let qi = new qItem(root, 1); q.push(qi); // Do level order traversal while (q.length != 0) { // Remove the front queue item qi = q.shift(); // Get details of the remove item let node = qi.node; let depth = qi.depth; // If this is the first leaf node seen so far // Then return its depth as answer if (node.left == null && node.right == null ) return depth; // If left subtree is not null, // add it to queue if (node.left != null ) { qi.node = node.left; qi.depth = depth + 1; q.push(qi); } // If right subtree is not null, // add it to queue if (node.right != null ) { qi.node = node.right; qi.depth = depth + 1; q.push(qi); } } return 0; } // Driver Code // Let us create binary tree shown // in above diagram let root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); document.write(minDepth(root)); // This code is contributed by rag2127 </script> |
输出:
2
另一种方法:
C++
/* C++ implementation to find minimum depth of a given Binary tree */ #include <iostream> #include<math.h> using namespace std; struct Node { int data; struct Node *left; struct Node *right; Node( int k){ data = k; left = right = NULL; } }; /* Function to calculate the minimum depth of the tree */ int minimumDepth(Node *root, int level) { if (root == NULL) return level; level++; return min(minimumDepth(root->left, level), minimumDepth(root->right, level)); } /* Driver program to test above functions */ int main() { // Let us create binary tree shown in above diagram Node *root = new Node(1); root->left = new Node(2); root->right = new Node(3); root->left->left = new Node(4); root->left->right = new Node(5); cout << minimumDepth(root, 0); return 0; } // This code is contributed by aafreen1804. |
JAVA
/* Java implementation to find minimum depth of a given Binary tree */ /* Class containing left and right child of current Node and key value*/ class Node { int data; Node left, right; public Node( int item) { data = item; left = right = null ; } } public class MinimumTreeHeight { // Root of the Binary Tree Node root; int minimumDepth() { return minimumDepth(root, 0 ); } /* Function to calculate the minimum depth of the tree */ int minimumDepth(Node root, int level) { if (root == null ) return level; level++; return Math.min(minimumDepth(root.left, level), minimumDepth(root.right, level)); } /* Driver program to test above functions */ public static void main(String args[]) { MinimumTreeHeight tree = new MinimumTreeHeight(); tree.root = new Node( 1 ); tree.root.left = new Node( 2 ); tree.root.right = new Node( 3 ); tree.root.left.left = new Node( 4 ); tree.root.left.right = new Node( 5 ); System.out.println( "The minimum depth of " + "binary tree is : " + tree.minimumDepth()); } } |
Python3
# Python implementation to find minimum depth # of a given Binary tree # Class containing left and right child of current # Node and key value class Node: # Constructor to create a new node def __init__( self , d): self .data = d self .left = None self .right = None # Function to calculate the minimum depth of the tree def minimumDepth(root, level): if (root = = None ): return level; level + = 1 ; return min (minimumDepth(root.left, level), minimumDepth(root.right, level)) # Driver program to test above functions root = Node( 1 ) root.left = Node( 2 ) root.right = Node( 3 ) root.left.left = Node( 4 ) root.left.right = Node( 5 ) print ( "The minimum depth of " , "binary tree is : " , minimumDepth(root, 0 )) # This code is contributed by ab2127 |
C#
/* C# implementation to find minimum depth of a given Binary tree */ using System; /* Class containing left and right child of current Node and key value*/ public class Node { public int data; public Node left, right; public Node( int item) { data = item; left = right = null ; } } public class MinimumTreeHeight { // Root of the Binary Tree Node root; int minimumDepth() { return minimumDepth(root, 0); } /* Function to calculate the minimum depth of the tree */ int minimumDepth(Node root, int level) { if (root == null ) return level; level++; return Math.Min(minimumDepth(root.left, level), minimumDepth(root.right, level)); } /* Driver code */ public static void Main(String[] args) { MinimumTreeHeight tree = new MinimumTreeHeight(); tree.root = new Node(1); tree.root.left = new Node(2); tree.root.right = new Node(3); tree.root.left.left = new Node(4); tree.root.left.right = new Node(5); Console.WriteLine( "The minimum depth of " + "binary tree is : " + tree.minimumDepth()); } } // This code has been contributed by 29AjayKumar |
Javascript
<script> /* Javascript implementation to find minimum depth of a given Binary tree */ /* Class containing left and right child of current Node and key value*/ class Node { constructor(item) { this .data=item; this .left= this .right= null ; } } // Root of the Binary Tree let root; /* Function to calculate the minimum depth of the tree */ function minimumDepths() { return minimumDepth(root, 0); } function minimumDepth(root,level) { if (root == null ) return level; level++; return Math.min(minimumDepth(root.left, level), minimumDepth(root.right, level)); } /* Driver program to test above functions */ root = new Node(1); root.left = new Node(2); root.right = new Node(3); root.left.left = new Node(4); root.left.right = new Node(5); document.write( "The minimum depth of " + "binary tree is : " + minimumDepths()); // This code is contributed by avanitrachhadiya2155 </script> |
输出:
The minimum depth of binary tree is : 2
感谢Manish Chauhan提出上述想法,感谢Ravi提供实施方案。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



