给定一棵二叉树,求最大路径和。路径可以从树中的任何节点开始和结束。 例子:
null
Input: Root of below tree 1 / 2 3Output: 6See below diagram for another example.1+2+3
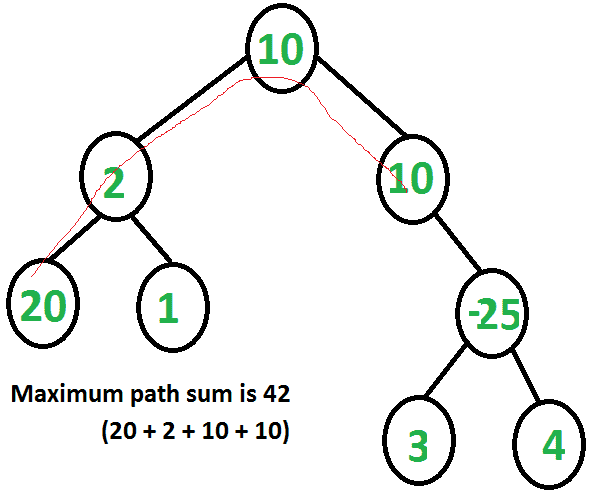
对于每个节点,最大路径可以通过四种方式通过节点: 1.仅限节点 2.通过左子节点+节点的最大路径 3.通过右子节点+节点的最大路径 4.通过左子节点的最大路径+节点+通过右子节点的最大路径 这样做的目的是跟踪四条路径,并最终选择最大路径。需要注意的一点是,每个子树的根都需要返回最大路径和,这样最多会涉及根的一个子树。这是父函数调用所必需的。在下面的代码中,该和存储在“max_single”中,并由递归函数返回。
C++
// C/C++ program to find maximum path sum in Binary Tree #include<bits/stdc++.h> using namespace std; // A binary tree node struct Node { int data; struct Node* left, *right; }; // A utility function to allocate a new node struct Node* newNode( int data) { struct Node* newNode = new Node; newNode->data = data; newNode->left = newNode->right = NULL; return (newNode); } // This function returns overall maximum path sum in 'res' // And returns max path sum going through root. int findMaxUtil(Node* root, int &res) { //Base Case if (root == NULL) return 0; // l and r store maximum path sum going through left and // right child of root respectively int l = findMaxUtil(root->left,res); int r = findMaxUtil(root->right,res); // Max path for parent call of root. This path must // include at-most one child of root int max_single = max(max(l, r) + root->data, root->data); // Max Top represents the sum when the Node under // consideration is the root of the maxsum path and no // ancestors of root are there in max sum path int max_top = max(max_single, l + r + root->data); res = max(res, max_top); // Store the Maximum Result. return max_single; } // Returns maximum path sum in tree with given root int findMaxSum(Node *root) { // Initialize result int res = INT_MIN; // Compute and return result findMaxUtil(root, res); return res; } // Driver program int main( void ) { struct Node *root = newNode(10); root->left = newNode(2); root->right = newNode(10); root->left->left = newNode(20); root->left->right = newNode(1); root->right->right = newNode(-25); root->right->right->left = newNode(3); root->right->right->right = newNode(4); cout << "Max path sum is " << findMaxSum(root); return 0; } |
JAVA
// Java program to find maximum path sum in Binary Tree /* Class containing left and right child of current node and key value*/ class Node { int data; Node left, right; public Node( int item) { data = item; left = right = null ; } } // An object of Res is passed around so that the // same value can be used by multiple recursive calls. class Res { public int val; } class BinaryTree { // Root of the Binary Tree Node root; // This function returns overall maximum path sum in 'res' // And returns max path sum going through root. int findMaxUtil(Node node, Res res) { // Base Case if (node == null ) return 0 ; // l and r store maximum path sum going through left and // right child of root respectively int l = findMaxUtil(node.left, res); int r = findMaxUtil(node.right, res); // Max path for parent call of root. This path must // include at-most one child of root int max_single = Math.max(Math.max(l, r) + node.data, node.data); // Max Top represents the sum when the Node under // consideration is the root of the maxsum path and no // ancestors of root are there in max sum path int max_top = Math.max(max_single, l + r + node.data); // Store the Maximum Result. res.val = Math.max(res.val, max_top); return max_single; } int findMaxSum() { return findMaxSum(root); } // Returns maximum path sum in tree with given root int findMaxSum(Node node) { // Initialize result // int res2 = Integer.MIN_VALUE; Res res = new Res(); res.val = Integer.MIN_VALUE; // Compute and return result findMaxUtil(node, res); return res.val; } /* Driver program to test above functions */ public static void main(String args[]) { BinaryTree tree = new BinaryTree(); tree.root = new Node( 10 ); tree.root.left = new Node( 2 ); tree.root.right = new Node( 10 ); tree.root.left.left = new Node( 20 ); tree.root.left.right = new Node( 1 ); tree.root.right.right = new Node(- 25 ); tree.root.right.right.left = new Node( 3 ); tree.root.right.right.right = new Node( 4 ); System.out.println( "maximum path sum is : " + tree.findMaxSum()); } } |
python
# Python program to find maximum path sum in Binary Tree # A Binary Tree Node class Node: # Constructor to create a new node def __init__( self , data): self .data = data self .left = None self .right = None # This function returns overall maximum path sum in 'res' # And returns max path sum going through root def findMaxUtil(root): # Base Case if root is None : return 0 # l and r store maximum path sum going through left # and right child of root respectively l = findMaxUtil(root.left) r = findMaxUtil(root.right) # Max path for parent call of root. This path # must include at most one child of root max_single = max ( max (l, r) + root.data, root.data) # Max top represents the sum when the node under # consideration is the root of the maxSum path and # no ancestor of root are there in max sum path max_top = max (max_single, l + r + root.data) # Static variable to store the changes # Store the maximum result findMaxUtil.res = max (findMaxUtil.res, max_top) return max_single # Return maximum path sum in tree with given root def findMaxSum(root): # Initialize result findMaxUtil.res = float ( "-inf" ) # Compute and return result findMaxUtil(root) return findMaxUtil.res # Driver program root = Node( 10 ) root.left = Node( 2 ) root.right = Node( 10 ); root.left.left = Node( 20 ); root.left.right = Node( 1 ); root.right.right = Node( - 25 ); root.right.right.left = Node( 3 ); root.right.right.right = Node( 4 ); print "Max path sum is " ,findMaxSum(root); # This code is contributed by Nikhil Kumar Singh(nickzuck_007) |
C#
// C# program to find maximum // path sum in Binary Tree using System; /* Class containing left and right child of current node and key value*/ public class Node { public int data; public Node left, right; public Node( int item) { data = item; left = right = null ; } } // An object of Res is passed // around so that the same value // can be used by multiple recursive calls. class Res { public int val; } public class BinaryTree { // Root of the Binary Tree Node root; // This function returns overall // maximum path sum in 'res' And // returns max path sum going through root. int findMaxUtil(Node node, Res res) { // Base Case if (node == null ) return 0; // l and r store maximum path // sum going through left and // right child of root respectively int l = findMaxUtil(node.left, res); int r = findMaxUtil(node.right, res); // Max path for parent call of root. // This path must include // at-most one child of root int max_single = Math.Max(Math.Max(l, r) + node.data, node.data); // Max Top represents the sum // when the Node under // consideration is the root // of the maxsum path and no // ancestors of root are there // in max sum path int max_top = Math.Max(max_single, l + r + node.data); // Store the Maximum Result. res.val = Math.Max(res.val, max_top); return max_single; } int findMaxSum() { return findMaxSum(root); } // Returns maximum path // sum in tree with given root int findMaxSum(Node node) { // Initialize result // int res2 = int.MinValue; Res res = new Res(); res.val = int .MinValue; // Compute and return result findMaxUtil(node, res); return res.val; } /* Driver code */ public static void Main(String []args) { BinaryTree tree = new BinaryTree(); tree.root = new Node(10); tree.root.left = new Node(2); tree.root.right = new Node(10); tree.root.left.left = new Node(20); tree.root.left.right = new Node(1); tree.root.right.right = new Node(-25); tree.root.right.right.left = new Node(3); tree.root.right.right.right = new Node(4); Console.WriteLine( "maximum path sum is : " + tree.findMaxSum()); } } // This code is contributed Rajput-Ji. |
Javascript
<script> // JavaScript program to find maximum // path sum in Binary Tree class Node { constructor(item) { this .left = null ; this .right = null ; this .data = item; } } let val; // Root of the Binary Tree let root; // This function returns overall maximum path sum in 'res' // And returns max path sum going through root. function findMaxUtil(node) { // Base Case if (node == null ) return 0; // l and r store maximum path sum going through left and // right child of root respectively let l = findMaxUtil(node.left); let r = findMaxUtil(node.right); // Max path for parent call of root. This path must // include at-most one child of root let max_single = Math.max(Math.max(l, r) + node.data, node.data); // Max Top represents the sum when the Node under // consideration is the root of the maxsum path and no // ancestors of root are there in max sum path let max_top = Math.max(max_single, l + r + node.data); // Store the Maximum Result. val = Math.max(val, max_top); return max_single; } function findMaxsum() { return findMaxSum(root); } // Returns maximum path sum in tree with given root function findMaxSum(node) { // Initialize result // int res2 = Integer.MIN_VALUE; val = Number.MIN_VALUE; // Compute and return result findMaxUtil(node); return val; } root = new Node(10); root.left = new Node(2); root.right = new Node(10); root.left.left = new Node(20); root.left.right = new Node(1); root.right.right = new Node(-25); root.right.right.left = new Node(3); root.right.right.right = new Node(4); document.write( "Max path sum is : " + findMaxsum()); </script> |
输出:
Max path sum is 42
时间复杂性: O(n),其中n是二叉树中的节点数。
本文由 安莫尔·瓦什尼 (FB简介: https://www.facebook.com/anmolvarshney695 )。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请发表评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



