给定两个数字 ![]() 和
和 ![]() .任务是找出 A. 可以用一个集合来表示
.任务是找出 A. 可以用一个集合来表示 ![]() 以至于
以至于 ![]() 这些数字之和等于 A. 而且
这些数字之和等于 A. 而且 ![]() (集合的最大大小不能超过 M ).
(集合的最大大小不能超过 M ).
null
例子 :
输入 :a=4,m=4 输出 : 2 –> ({4}, {3, 1}) 笔记 :{2,2}不是有效集,因为值不是按降序排列的
输入 :a=7,m=5 输出 : 5 –> ({7}, {6, 1}, {5, 2}, {4, 3}, {4, 2, 1})
方法: 这个问题可以通过使用递归方法进行分治来解决,该方法遵循以下条件:
- 如果 A. 等于零,则找到一个解。
- 如果a>0且m==0,则此集合违反条件,因为无法在集合中添加更多值。
- 如果已经对给定的 A. , M 和prev(当前集合中包含的最后一个值)返回该值。
- 从…开始循环 我 = A. 直到0,如果 我 < 上 ,如果我们包括 我 在当前集合中,并返回它。
以下是上述方法的实施情况:
# Python3 code to calculate the number of ways # in which a given number can be represented # as set of finite numbers # Import function to initialize the dictionary from collections import defaultdict # Initialize dictionary which is used # to check if given solution is already # visited or not to avoid # calculating it again visited = defaultdict( lambda : False ) # Initialize dictionary which is used to # store the number of ways in which solution # can be obtained for given values numWays = defaultdict( lambda : 0 ) # This function returns the total number # of sets which satisfy given criteria # a --> number to be divided into sets # m --> maximum possible size of the set # x --> previously selected value def countNumOfWays(a, m, prev): # number is divided properly and # hence solution is obtained if a = = 0 : return 1 # Solution can't be obtained elif a > 0 and m = = 0 : return 0 # Return the solution if it has # already been calculated elif visited[(a, m, prev)] = = True : return numWays[(a, m, prev)] else : visited[(a, m, prev)] = True for i in range (a, - 1 , - 1 ): # Continue only if current value is # smaller compared to previous value if i < prev: numWays[(a,m,prev)] + = countNumOfWays(a - i,m - 1 ,i) return numWays[(a, m, prev)] # Values of 'a' and 'm' for which # solution is to be found # MAX_CONST is extremely large value # used for first comparison in the function a, m, MAX_CONST = 7 , 5 , 10 * * 5 print (countNumOfWays(a, m, MAX_CONST)) |
输出:
5
时间复杂性: O(a*log(a))
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
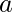


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)