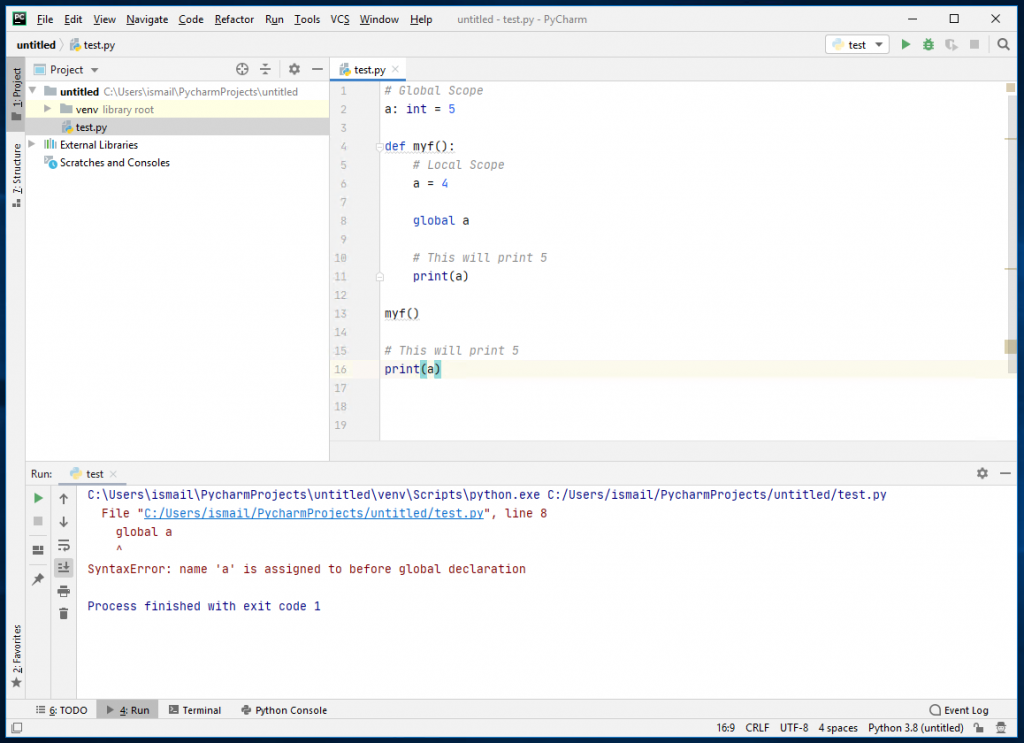
先决条件: C/C中的指针++
原因可能有很多,但这里有两个原因:
理由1: 考虑INTARR〔100〕。答案在于编译器如何解释arr[i](0<=i<100)。 arr[i]被解释为*(arr+i)。现在,arr是数组的地址或数组的第0个索引元素的地址。所以,数组中下一个元素的地址是arr+1(因为数组中的元素存储在连续的内存位置),下一个位置的地址是arr+2,依此类推。根据以上参数,arr+i是指距离数组起始元素i距离处的地址。因此,根据这个定义,数组的起始元素i将为零,因为起始元素与数组的起始元素的距离为0。为了符合arr[i]的定义,数组的索引从0开始。
CPP
#include<iostream> using namespace std; int main() { int arr[] = {1, 2, 3, 4}; // Below two statements mean same thing cout << *(arr + 1) << " " ; cout << arr[1] << " " ; return 0; } |
2 2
结论是,我们需要阵列中的随机访问。为了提供随机访问,编译器使用指针算法到达第i个元素。
理由2:
现代语言,尤其是 C++ 使用row-major 存储二维数组的顺序。
让我们假设一个2D数组,用两种不同的方法编写一个行主公式:
- 从1开始的数组索引
- 从0开始的数组索引
让2D数组为int类型的arr[m][n]
让&arr成为“地址”
案例1(数组索引从1开始):
&(arr[i][j])=address+[(i-1)*n+(j-1)]*(sizeof(int))]所以我们在这里执行6个操作
案例2(数组索引从0开始):
&(arr[i][j])=address+[(i)*n+(j)]*(sizeof(int)),这里我们只执行4个操作
所以我们在这里看到,当我们存储2D数组并获取一个元素的地址时,我们执行的操作少了2个。这看起来没有道理,但确实有道理!在处理海量数据时,这可能会提高性能和速度。 案例1 可能看起来很友好,但是 案例2 效率更高。这就是为什么大多数语言都喜欢 C++、Python、java 使用从索引0开始的数组,很少使用像 卢阿 以索引1开头的数组。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)