统计数字 该模块提供了非常强大的工具,可以用来计算任何与统计相关的数据。 方差() 就是这样一种功能。此函数有助于计算数据样本的方差(样本是填充数据的子集)。 方差() 函数只应在需要计算样本方差时使用。还有另一个函数称为pvariance(),用于计算整个群体的方差。 在纯统计学中,方差是变量与其均值的平方偏差。基本上,它根据随机数据的平均值或中值来衡量随机数据在集合中的传播。方差的低值表示数据聚集在一起,并且没有广泛分布,而高值表示给定集合中的数据比平均值分布更广。 方差是科学中的一个重要工具,在科学中,数据的统计分析很常见。它是给定数据集标准偏差的平方,也称为分布的第二中心矩。它通常由 ![]() 在纯统计中。 方差通过以下公式计算:
在纯统计中。 方差通过以下公式计算:
它是通过平方的平均值减去平方的平均值来计算的
![Rendered by QuickLaTeX.com operatorname {Var} (X)=operatorname {E} left[(X-mu )^{2}
ight]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-38400e88345e9f8b94d105ba1256c262_l3.png)
语法: 方差([数据],xbar) 参数: [数据]: 具有实数的可数。 xbar(可选): 将数据集的实际平均值作为值。 返回类型: 返回作为参数传递的值的实际方差。 例外情况: 统计误差 对于作为参数传递的小于2个值的数据集引发。 当提供的值为 xbar 与数据集的实际平均值不匹配。
代码#1:
Python3
# Python code to demonstrate the working of # variance() function of Statistics Module # Importing Statistics module import statistics # Creating a sample of data sample = [ 2.74 , 1.23 , 2.63 , 2.22 , 3 , 1.98 ] # Prints variance of the sample set # Function will automatically calculate # it's mean and set it as xbar print ( "Variance of sample set is % s" % (statistics.variance(sample))) |
输出:
Variance of sample set is 0.40924
代码#2: 在一系列数据类型上演示variance()
Python3
# Python code to demonstrate variance() # function on varying range of data-types # importing statistics module from statistics import variance # importing fractions as parameter values from fractions import Fraction as fr # tuple of a set of positive integers # numbers are spread apart but not very much sample1 = ( 1 , 2 , 5 , 4 , 8 , 9 , 12 ) # tuple of a set of negative integers sample2 = ( - 2 , - 4 , - 3 , - 1 , - 5 , - 6 ) # tuple of a set of positive and negative numbers # data-points are spread apart considerably sample3 = ( - 9 , - 1 , - 0 , 2 , 1 , 3 , 4 , 19 ) # tuple of a set of fractional numbers sample4 = (fr( 1 , 2 ), fr( 2 , 3 ), fr( 3 , 4 ), fr( 5 , 6 ), fr( 7 , 8 )) # tuple of a set of floating point values sample5 = ( 1.23 , 1.45 , 2.1 , 2.2 , 1.9 ) # Print the variance of each samples print ( "Variance of Sample1 is % s " % (variance(sample1))) print ( "Variance of Sample2 is % s " % (variance(sample2))) print ( "Variance of Sample3 is % s " % (variance(sample3))) print ( "Variance of Sample4 is % s " % (variance(sample4))) print ( "Variance of Sample5 is % s " % (variance(sample5))) |
输出:
Variance of Sample 1 is 15.80952380952381 Variance of Sample 2 is 3.5 Variance of Sample 3 is 61.125 Variance of Sample 4 is 1/45 Variance of Sample 5 is 0.17613000000000006
代码#3: 演示xbar参数的使用
Python3
# Python code to demonstrate # the use of xbar parameter # Importing statistics module import statistics # creating a sample list sample = ( 1 , 1.3 , 1.2 , 1.9 , 2.5 , 2.2 ) # calculating the mean of sample set m = statistics.mean(sample) # calculating the variance of sample set print ( "Variance of Sample set is % s" % (statistics.variance(sample, xbar = m))) |
输出:
Variance of Sample set is 0.3656666666666667
代码#4: 演示当 xbar 与平均值/平均值不同
Python3
# Python code to demonstrate the error caused # when garbage value of xbar is entered # Importing statistics module import statistics # creating a sample list sample = ( 1 , 1.3 , 1.2 , 1.9 , 2.5 , 2.2 ) # calculating the mean of sample set m = statistics.mean(sample) # Actual value of mean after calculation # comes out to 1.6833333333333333 # But to demonstrate xbar error let's enter # -100 as the value for xbar parameter print (statistics.variance(sample, xbar = - 100 )) |
输出:
0.3656666666663053
注:其精度与代码#3中的输出不同 代码#4: 显示统计错误
Python3
# Python code to demonstrate StatisticsError # importing Statistics module import statistics # creating an empty data-srt sample = [] # will raise Statistics Error print (statistics.variance(sample)) |
输出:
Traceback (most recent call last): File "/home/64bf6d80f158b65d2b75c894d03a7779.py", line 10, in print(statistics.variance(sample)) File "/usr/lib/python3.5/statistics.py", line 555, in variance raise StatisticsError('variance requires at least two data points')statistics.StatisticsError: variance requires at least two data points
应用: 方差是统计和处理大量数据的一个非常重要的工具。比如,当全知均值未知(样本均值)时,方差被用作有偏估计量。现实世界中的观察结果,比如一家公司全天所有股票的涨跌值,并不是所有可能的观察结果。因此,方差是从一组有限的数据中计算出来的,尽管考虑到整个人群时,方差不会匹配,但它仍然会给用户提供一个估计值,足以计算出其他计算结果。
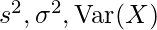


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)