康威（Python的游戏实现）-yiteyi-C++库

康威的生命游戏是约翰·康威创造的一种细胞自动化方法。这个游戏是在考虑生物学的基础上创建的，但已经被应用于各种领域，如图形、地形生成等。。

null

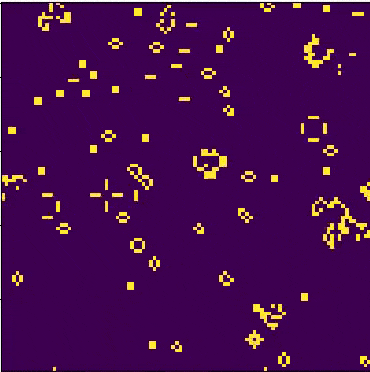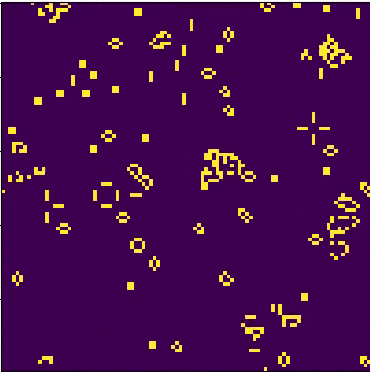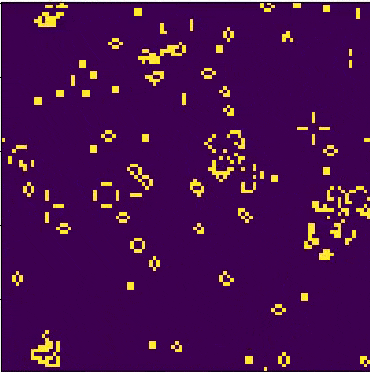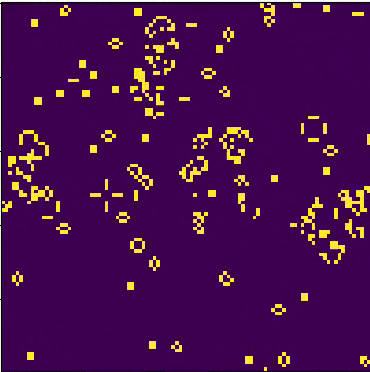
life_game

“游戏”是一个零人游戏，这意味着它的进化是由它的初始状态决定的，不需要进一步的输入。一个人通过创建一个初始配置并观察其演变来与生命游戏互动，或者，对于高级“玩家”，通过创建具有特定属性的模式。 游戏如何运作 因为生命的游戏是建立在一个由九个正方形组成的网格上的，每个单元格都有八个相邻的单元格，如给定的图所示。模拟中的给定单元格（i，j）是在网格[i][j]上访问的，其中i和j分别是行和列索引。给定单元在给定时刻的值取决于其相邻单元在上一时间步的状态。康威的人生游戏有四条规则。

如果一个单元格处于打开状态，并且只有不到两个邻居处于打开状态，则该单元格将关闭
如果一个单元处于打开状态，并且有两个或三个相邻单元处于打开状态，则该单元将保持打开状态。
如果一个单元处于打开状态，并且有三个以上的邻居处于打开状态，则该单元将关闭。
如果一个单元处于关闭状态，且恰好有三个邻居处于打开状态，则该单元将打开。

图片[2]-康威（Python的游戏实现）-yiteyi-C++库

既然我们知道它是如何工作的，接下来我们需要弄清楚如何让它工作。方法

1. Initialize the cells in the grid.2. At each time step in the simulation, for each    cell (i, j) in the grid, do the following:   a. Update the value of cell (i, j) based on       its neighbors, taking into account the       boundary conditions.   b. Update the display of grid values.

完成后，让我们着手编写代码。要求

努比
matplotlib
argparse
皮加梅

现在让我们开始吧密码

Python3

                         # Python code to implement Conway's Game Of Life                       
                         import                                     argparse                       
                         import                                     numpy as np                       
                         import                                     matplotlib.pyplot as plt                       
                         import                                     matplotlib.animation as animation                       
           
                         # setting up the values for the grid                       
                         ON                                     =                                     255                       
                         OFF                                     =                                     0                       
                         vals                                     =                                     [ON, OFF]                       
           
                         def                                     randomGrid(N):                       
           
                                                 """returns a grid of NxN random values"""                       
                                                 return                                     np.random.choice(vals, N                                     *                                     N, p                                     =                                     [                                     0.2                                     ,                                     0.8                                     ]).reshape(N, N)                       
           
                         def                                     addGlider(i, j, grid):                       
           
                                                 """adds a glider with top left cell at (i, j)"""                       
                                                 glider                                     =                                     np.array([[                                     0                                     ,                                     0                                     ,                                     255                                     ],                       
                                                 [                                     255                                     ,                                     0                                     ,                                     255                                     ],                       
                                                 [                                     0                                     ,                                     255                                     ,                                     255                                     ]])                       
                                                 grid[i:i                                     +                                     3                                     , j:j                                     +                                     3                                     ]                                     =                                     glider                       
           
                         def                                     addGosperGliderGun(i, j, grid):                       
           
                                                 """adds a Gosper Glider Gun with top left                       
                                                 cell at (i, j)"""                       
                                                 gun                                     =                                     np.zeros(                                     11                                     *                                     38                                     ).reshape(                                     11                                     ,                                     38                                     )                       
           
                                                 gun[                                     5                                     ][                                     1                                     ]                                     =                                     gun[                                     5                                     ][                                     2                                     ]                                     =                                     255                       
                                                 gun[                                     6                                     ][                                     1                                     ]                                     =                                     gun[                                     6                                     ][                                     2                                     ]                                     =                                     255                       
           
                                                 gun[                                     3                                     ][                                     13                                     ]                                     =                                     gun[                                     3                                     ][                                     14                                     ]                                     =                                     255                       
                                                 gun[                                     4                                     ][                                     12                                     ]                                     =                                     gun[                                     4                                     ][                                     16                                     ]                                     =                                     255                       
                                                 gun[                                     5                                     ][                                     11                                     ]                                     =                                     gun[                                     5                                     ][                                     17                                     ]                                     =                                     255                       
                                                 gun[                                     6                                     ][                                     11                                     ]                                     =                                     gun[                                     6                                     ][                                     15                                     ]                                     =                                     gun[                                     6                                     ][                                     17                                     ]                                     =                                     gun[                                     6                                     ][                                     18                                     ]                                     =                                     255                       
                                                 gun[                                     7                                     ][                                     11                                     ]                                     =                                     gun[                                     7                                     ][                                     17                                     ]                                     =                                     255                       
                                                 gun[                                     8                                     ][                                     12                                     ]                                     =                                     gun[                                     8                                     ][                                     16                                     ]                                     =                                     255                       
                                                 gun[                                     9                                     ][                                     13                                     ]                                     =                                     gun[                                     9                                     ][                                     14                                     ]                                     =                                     255                       
           
                                                 gun[                                     1                                     ][                                     25                                     ]                                     =                                     255                       
                                                 gun[                                     2                                     ][                                     23                                     ]                                     =                                     gun[                                     2                                     ][                                     25                                     ]                                     =                                     255                       
                                                 gun[                                     3                                     ][                                     21                                     ]                                     =                                     gun[                                     3                                     ][                                     22                                     ]                                     =                                     255                       
                                                 gun[                                     4                                     ][                                     21                                     ]                                     =                                     gun[                                     4                                     ][                                     22                                     ]                                     =                                     255                       
                                                 gun[                                     5                                     ][                                     21                                     ]                                     =                                     gun[                                     5                                     ][                                     22                                     ]                                     =                                     255                       
                                                 gun[                                     6                                     ][                                     23                                     ]                                     =                                     gun[                                     6                                     ][                                     25                                     ]                                     =                                     255                       
                                                 gun[                                     7                                     ][                                     25                                     ]                                     =                                     255                       
           
                                                 gun[                                     3                                     ][                                     35                                     ]                                     =                                     gun[                                     3                                     ][                                     36                                     ]                                     =                                     255                       
                                                 gun[                                     4                                     ][                                     35                                     ]                                     =                                     gun[                                     4                                     ][                                     36                                     ]                                     =                                     255                       
           
                                                 grid[i:i                                     +                                     11                                     , j:j                                     +                                     38                                     ]                                     =                                     gun                       
           
                         def                                     update(frameNum, img, grid, N):                       
           
                                                 # copy grid since we require 8 neighbors                       
                                                 # for calculation and we go line by line                       
                                                 newGrid                                     =                                     grid.copy()                       
                                                 for                                     i                                     in                                     range                                     (N):                       
                                                 for                                     j                                     in                                     range                                     (N):                       
           
                                                 # compute 8-neighbor sum                       
                                                 # using toroidal boundary conditions - x and y wrap around                       
                                                 # so that the simulaton takes place on a toroidal surface.                       
                                                 total                                     =                                     int                                     ((grid[i, (j                                     -                                     1                                     )                                     %                                     N]                                     +                                     grid[i, (j                                     +                                     1                                     )                                     %                                     N]                                     +                       
                                                 grid[(i                                     -                                     1                                     )                                     %                                     N, j]                                     +                                     grid[(i                                     +                                     1                                     )                                     %                                     N, j]                                     +                       
                                                 grid[(i                                     -                                     1                                     )                                     %                                     N, (j                                     -                                     1                                     )                                     %                                     N]                                     +                                     grid[(i                                     -                                     1                                     )                                     %                                     N, (j                                     +                                     1                                     )                                     %                                     N]                                     +                       
                                                 grid[(i                                     +                                     1                                     )                                     %                                     N, (j                                     -                                     1                                     )                                     %                                     N]                                     +                                     grid[(i                                     +                                     1                                     )                                     %                                     N, (j                                     +                                     1                                     )                                     %                                     N])                                     /                                     255                                     )                       
           
                                                 # apply Conway's rules                       
                                                 if                                     grid[i, j]                                     =                                     =                                     ON:                       
                                                 if                                     (total <                                     2                                     )                                     or                                     (total >                                     3                                     ):                       
                                                 newGrid[i, j]                                     =                                     OFF                       
                                                 else                                     :                       
                                                 if                                     total                                     =                                     =                                     3                                     :                       
                                                 newGrid[i, j]                                     =                                     ON                       
           
                                                 # update data                       
                                                 img.set_data(newGrid)                       
                                                 grid[:]                                     =                                     newGrid[:]                       
                                                 return                                     img,                       
           
                         # main() function                       
                         def                                     main():                       
           
                                                 # Command line args are in sys.argv[1], sys.argv[2] ..                       
                                                 # sys.argv[0] is the script name itself and can be ignored                       
                                                 # parse arguments                       
                                                 parser                                     =                                     argparse.ArgumentParser(description                                     =                                     "Runs Conway's Game of Life simulation."                                     )                       
           
                                                 # add arguments                       
                                                 parser.add_argument(                                     '--grid-size'                                     , dest                                     =                                     'N'                                     , required                                     =                                     False                                     )                       
                                                 parser.add_argument(                                     '--mov-file'                                     , dest                                     =                                     'movfile'                                     , required                                     =                                     False                                     )                       
                                                 parser.add_argument(                                     '--interval'                                     , dest                                     =                                     'interval'                                     , required                                     =                                     False                                     )                       
                                                 parser.add_argument(                                     '--glider'                                     , action                                     =                                     'store_true'                                     , required                                     =                                     False                                     )                       
                                                 parser.add_argument(                                     '--gosper'                                     , action                                     =                                     'store_true'                                     , required                                     =                                     False                                     )                       
                                                 args                                     =                                     parser.parse_args()                       
                                   
                                                 # set grid size                       
                                                 N                                     =                                     100                       
                                                 if                                     args.N                                     and                                     int                                     (args.N) >                                     8                                     :                       
                                                 N                                     =                                     int                                     (args.N)                       
                                   
                                                 # set animation update interval                       
                                                 updateInterval                                     =                                     50                       
                                                 if                                     args.interval:                       
                                                 updateInterval                                     =                                     int                                     (args.interval)                       
           
                                                 # declare grid                       
                                                 grid                                     =                                     np.array([])                       
           
                                                 # check if "glider" demo flag is specified                       
                                                 if                                     args.glider:                       
                                                 grid                                     =                                     np.zeros(N                                     *                                     N).reshape(N, N)                       
                                                 addGlider(                                     1                                     ,                                     1                                     , grid)                       
                                                 elif                                     args.gosper:                       
                                                 grid                                     =                                     np.zeros(N                                     *                                     N).reshape(N, N)                       
                                                 addGosperGliderGun(                                     10                                     ,                                     10                                     , grid)                       
           
                                                 else                                     :                                     # populate grid with random on/off -                       
                                                 # more off than on                       
                                                 grid                                     =                                     randomGrid(N)                       
           
                                                 # set up animation                       
                                                 fig, ax                                     =                                     plt.subplots()                       
                                                 img                                     =                                     ax.imshow(grid, interpolation                                     =                                     'nearest'                                     )                       
                                                 ani                                     =                                     animation.FuncAnimation(fig, update, fargs                                     =                                     (img, grid, N, ),                       
                                                 frames                                     =                                     10                                     ,                       
                                                 interval                                     =                                     updateInterval,                       
                                                 save_count                                     =                                     50                                     )                       
           
                                                 # # of frames?                       
                                                 # set output file                       
                                                 if                                     args.movfile:                       
                                                 ani.save(args.movfile, fps                                     =                                     30                                     , extra_args                                     =                                     [                                     '-vcodec'                                     ,                                     'libx264'                                     ])                       
           
                                                 plt.show()                       
           
                         # call main                       
                         if                                     __name__                                     =                                     =                                     '__main__'                                     :                       
                                                 main()                       

不传递任何命令行参数。

现在让我们稍微放大一些，让我们看看如果add每500毫秒更新一次动画，设置尺寸32X32，并使用初始的滑翔机模式，会发生什么。

python 'filename.py' --grid-size 32 --interval 500 --glider

您可以尝试使用此代码创建不同的模拟。 参考链接：

本文的Github代码
书籍：Python游乐场：好奇程序员的极客项目
努比医生
matplotlib文档

本文由 Subhajit Saha .如果你喜欢GeekSforgek，并且想投稿，你也可以邮寄你的文章进行评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

Python