模拟非确定性有限自动机（NFA）的C程序-yiteyi-C++库

出身背景

null

NFA通常使用有向图来描述。每个边和顶点都标记为0或1，表示可能的过渡。顶点表示NFA的状态。标记为0的是非接受状态，标记为1的是接受状态。

它需要一个有限长度的输入字符串。通常，输入字符串是0和1的二进制序列。
我们从顶点1开始，它始终是起始状态，然后按照输入字符串的位顺序指定的边，直到输入字符串没有其他位为止。
术语“非确定性”意味着在任何状态下，我们都有一个以上的选择来跟随一条边。NFA使用输入字符串，状态集Q表示NFA的可能移动。
如果Q至少包含一个最后一个顶点接受的状态，那么我们说NFA接受了输入字符串，否则NFA拒绝了输入字符串。
每个NFA都不是DFA，但每个NFA都可以翻译成DFA。

NFA的例子：

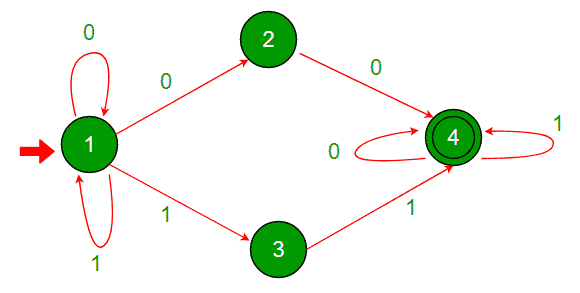
Starting state - vertex 1Accepting states - Vertices with double circles(label 1) // Vertex 4Non accepting states - single circles (label 0). // Vertices 1, 2 and 3.

如何检查字符串的验收？

输入：1010

在状态1中，我们有两种可能性，要么跟随自循环并保持在状态1，要么跟随标记为1的边并进入状态3。

                            {1} 1010 --> {1, 3} 010

在状态3中，没有标记为0的边，因此计算将消失。
在状态1中，我们有两种可能，要么跟随自循环并保持在状态1，要么跟随标记为0的边到状态2。

                            {1, 3} 010 --> {1, 2} 10

现在，状态2没有标记为1的边。计算将消失。我们有两种可能性：要么跟随自循环到状态1，要么跟随标记为1的边到状态3。

                             {1, 2} 10 --> {1, 3} 0

在状态3中，没有标记为0的边。因此，计算将消失。在状态1中，我们有两种可能性：要么跟随自循环到状态1，要么跟随标记为0的边到状态2。

                                 {1, 3} 0 --> {1, 2}

现在NFA已经消耗了输入。它可以处于状态1或状态2，这两种状态都是不可接受的。所以 NFA已拒绝输入1010。

输入：1100

          {1} 1100 --> {1, 3} 100 {1, 3} 100 --> {1, 3, 4} 00 {1, 3, 4}                   00--> {1, 2, 4} 0 {1, 2, 4} 0--> {1, 2, 4}

现在NFA已经消耗了输入。它可以处于状态1、2或4。第四州是一个接受州。所以 NFA接受字符串1100。
我们可以很容易地验证给定的NFA是否接受所有以“00”和/或“11”作为子字符串的二进制字符串。

模拟非确定性有限自动机（NFA）的C程序

输入格式： NFA的邻接列表表示形式如下所示。给出的示例将表示为边缘总数：4 边缘连接： 1 0 4 0 1 0 2 1 1 1 3 2 0 1 0 4 3 0 1 1 4 4 1 2 0 4 1 4

输出格式： NFA按照字典顺序接受的前10个二进制字符串（e表示空字符串）：{e，0，1，00，01，10，11000，…}

给定测试用例的样本输出如下： 00 11 000 001 011 100 110 111

C

                         #include <stdio.h>                       
                         #include <stdlib.h>                       
                         #include <string.h>                       
                         #include <stdbool.h>                       
                         #include <math.h>                       
           
                         int                                     row = 0;                       
           
                         // A structure to represent an adjacency list node                       
                         struct                                     node                       
                         {                       
                                                 int                                     data;                       
                                                 struct                                     node* next;                       
                                                 char                                     edgetype;                       
           
                         }                                     typedef                                     node;                       
           
                         // Adds an edge to an adjacency list                       
                         node* push(node* first ,                                     char                                     edgetype ,                                     int                                     data)                       
                         {                       
                                                 node* new_node = (node*)                                     malloc                                     (                                     sizeof                                     (node));                       
                                                 new_node->edgetype = edgetype;                       
                                                 new_node->data = data;                       
                                                 new_node->next = NULL;                       
                                                 if                                     (first==NULL)                       
                                                 {                       
                                                 first = new_node;                       
                                                 return                                     new_node;                       
                                                 }                       
                                                 first->next = push(first->next,edgetype,data);                       
                                                 return                                     first;                       
                         }                       
           
                         //Recursive function to check acceptance of input                       
                         int                                     nfa(node** graph,                                     int                                     current,                                     char                                     * input,                       
                                                 int                                     * accept,                                     int                                     start)                       
                         {                       
                                                 if                                     (start==(                                     int                                     )                                     strlen                                     (input))                       
                                                 return                                     accept[current];                       
           
                                                 node* temp = graph[current];                       
                                                 while                                     (temp != NULL)                       
                                                 {                       
                                                 if                                     (input[start]==temp->edgetype)                       
                                                 if                                     (nfa(graph,temp->data,input,accept,start+1==1))                       
                                                 return                                     1;                       
                                                 temp=temp->next;                       
                                                 }                       
                                                 return                                     0;                       
                         }                       
           
                         //Function to generate binary strings of size n                       
                         void                                     generate(                                     char                                     ** arr,                                     int                                     size,                                     char                                     *a)                       
                         {                       
                                                 if                                     (size==0)                       
                                                 {                       
                                                 strcpy                                     (arr[row], a);                       
                                                 row++;                       
                                                 return                                     ;                       
                                                 }                       
                                                 char                                     b0[20] = {                                     ' '                                     };                       
                                                 char                                     b1[20] = {                                     ' '                                     };                       
                                                 b0[0] =                                     '0'                                     ;                       
                                                 b1[0] =                                     '1'                                     ;                       
           
                                                 //Recursively generate the binary string                       
                                                 generate((                                     char                                     **)arr, size-1,                                     strcat                                     (b0,a));                                     //Add 0 in front                       
                                                 generate((                                     char                                     **)arr, size-1,                                     strcat                                     (b1,a));                                     //Add 1 in front                       
                                                 return                                     ;                       
           
                         }                       
           
                         // Driver program to test above functions                       
                         int                                     main()                       
                         {                       
                                                 int                                     n;                       
                                                 int                                     i, j;                       
                                                 scanf                                     (                                     "%d"                                     , &n);                                     //Number of nodes                       
                                                 node* graph[n+1];                                     //Create a graph                       
           
                                                 for                                     (i=0;i<n+1;i++)                       
                                                 graph[i]=NULL;                       
           
           
                                                 int                                     accept[n+1];                                     //Array to store state of vertex                       
           
                                                 for                                     (i=0; i<n; i++)                       
                                                 {                       
                                                 //Index of vertex , Acceptance state , Number of edges                       
                                                 int                                     index,acc,number_nodes;                       
                                                 scanf                                     (                                     "%d%d%d"                                     ,&index,&acc,&number_nodes);                       
                                                 accept[index]=acc;                                     //Store acceptance                       
           
                                                 for                                     (j=0;j<number_nodes;j++)                                     //Add all edges                       
                                                 {                       
                                                 int                                     node_add;                       
                                                 int                                     edge;                       
                                                 scanf                                     (                                     "%d%d"                                     ,&edge,&node_add);                       
                                                 graph[index] = push(graph[index],                                     '0'                                     +edge,node_add);                       
                                                 }                       
                                                 }                       
           
                                                 int                                     size = 1;                                     //Size of input                       
                                                 int                                     count = 0;                                     //Keep count of output strings                       
           
                                                 if                                     (accept[1]==1)                                     //Check for empty string                       
                                                 {                       
                                                 printf                                     (                                     "e"                                     );                       
                                                 count++;                       
                                                 }                       
           
                                                 while                                     (count < 11)                       
                                                 {                       
                                                 char                                     ** arr;                       
                                                 int                                     power =                                     pow                                     (2,size);                       
                                                 arr = (                                     char                                     **)                                     malloc                                     (power*                                     sizeof                                     (                                     char                                     *));                       
           
                                                 for                                     (i=0;i<power;i++)                       
                                                 arr[i] = (                                     char                                     *)                                     malloc                                     (size*                                     sizeof                                     (                                     char                                     ));                       
           
                                                 char                                     a[20] = {                                     ' '                                     };                       
           
                                                 generate((                                     char                                     **)arr,size,a);                                     //Generate inputs                       
           
                                                 for                                     (i=0; i<power; i++)                       
                                                 {                       
                                                 char                                     input[20] = {                                     ' '                                     };                       
           
                                                 for                                     (j=0; j<size; j++)                       
                                                 {                       
                                                 char                                     foo[2];                       
                                                 foo[0] = arr[i][size-1-j];                       
                                                 foo[1] =                                     ' '                                     ;                       
                                                 strcat                                     (input,foo);                       
                                                 //Copy generated string input                       
                                                 }                       
           
                                                 int                                     result = nfa(graph,1,input,accept,0);                       
                                                 // Store result of nfa                       
           
                                                 if                                     (result==1)                       
                                                 {                       
                                                 printf                                     (                                     "%s"                                     ,input);                       
                                                 // Print if accepted                       
                                                 count++;                       
                                                 }                       
           
                                                 if                                     (count==10)                       
                                                 return                                     0;                       
                                                 }                       
           
                                                 size++;                                     //Increment size of binary string input                       
                                                 row=0;                       
                                                 }                       
           
                                                 return                                     0;                       
                         }                       

输入：

41 0 4 0 1 0 2 1 1 1 32 0 1 0 43 0 1 1 44 1 2 0 4 1 4

输出：

001100000101110011011100000001

本文由 阿尔琼·穆尔拉贾尼。 如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论

文章版权归作者所有，未经允许请勿转载。

THE END