我们得到了两个排序数组。我们需要合并这两个数组,以便初始数字(在完成排序后)在第一个数组中,其余数字在第二个数组中。O(1)中允许的额外空间。
例子:
Input: ar1[] = {10}; ar2[] = {2, 3};Output: ar1[] = {2} ar2[] = {3, 10} Input: ar1[] = {1, 5, 9, 10, 15, 20}; ar2[] = {2, 3, 8, 13};Output: ar1[] = {1, 2, 3, 5, 8, 9} ar2[] = {10, 13, 15, 20}
如果允许我们使用额外的空间,这个任务很简单,并且是O(m+n)。但如果不允许额外的空间,而且在不到O(m*n)的最坏情况下看起来不可能,情况就会变得非常复杂。尽管进一步的优化是可能的 我们的想法是从ar2[]的最后一个元素开始,在ar1[]中搜索它。如果ar1[]中有一个更大的元素,那么我们将ar1[]的最后一个元素移动到ar2[]。为了保持ar1[]和ar2[]的排序,我们需要将ar2[]的最后一个元素放置在ar1[]中的正确位置。我们可以使用 插入排序 此文件的插入类型。
1.方法1
算法:
1) Iterate through every element of ar2[] starting from last element. Do following for every element ar2[i] a) Store last element of ar1[i]: last = ar1[i] b) Loop from last element of ar1[] while element ar1[j] is greater than ar2[i]. ar1[j+1] = ar1[j] // Move element one position ahead j-- c) If any element of ar1[] was moved or (j != m-1) ar1[j+1] = ar2[i] ar2[i] = last
在上面的循环中,ar1[]和ar2[]中的元素始终保持排序。
下面是上述算法的实现。
C++
// C++ program to merge two sorted // arrays with O(1) extra space. #include <bits/stdc++.h> using namespace std; // Merge ar1[] and ar2[] with O(1) extra space void merge( int ar1[], int ar2[], int m, int n) { // Iterate through all elements // of ar2[] starting from the last element for ( int i = n - 1; i >= 0; i--) { /* Find the smallest element greater than ar2[i]. Move all elements one position ahead till the smallest greater element is not found */ int j, last = ar1[m - 1]; for (j = m - 2; j >= 0 && ar1[j] > ar2[i]; j--) ar1[j + 1] = ar1[j]; // If there was a greater element if (j != m - 2 || last > ar2[i]) { ar1[j + 1] = ar2[i]; ar2[i] = last; } } } // Driver program int main() { int ar1[] = { 1, 5, 9, 10, 15, 20 }; int ar2[] = { 2, 3, 8, 13 }; int m = sizeof (ar1) / sizeof (ar1[0]); int n = sizeof (ar2) / sizeof (ar2[0]); merge(ar1, ar2, m, n); cout << "After Merging nFirst Array: " ; for ( int i = 0; i < m; i++) cout << ar1[i] << " " ; cout << "nSecond Array: " ; for ( int i = 0; i < n; i++) cout << ar2[i] << " " ; return 0; } |
JAVA
// Java program program to merge two // sorted arrays with O(1) extra space. import java.util.Arrays; class Test { static int arr1[] = new int []{ 1 , 5 , 9 , 10 , 15 , 20 }; static int arr2[] = new int []{ 2 , 3 , 8 , 13 }; static void merge( int m, int n) { // Iterate through all elements of ar2[] starting from // the last element for ( int i=n- 1 ; i>= 0 ; i--) { /* Find the smallest element greater than ar2[i]. Move all elements one position ahead till the smallest greater element is not found */ int j, last = arr1[m- 1 ]; for (j=m- 2 ; j >= 0 && arr1[j] > arr2[i]; j--) arr1[j+ 1 ] = arr1[j]; // If there was a greater element if (j != m- 2 || last > arr2[i]) { arr1[j+ 1 ] = arr2[i]; arr2[i] = last; } } } // Driver method to test the above function public static void main(String[] args) { merge(arr1.length,arr2.length); System.out.print( "After Merging nFirst Array: " ); System.out.println(Arrays.toString(arr1)); System.out.print( "Second Array: " ); System.out.println(Arrays.toString(arr2)); } } |
Python3
# Python program to merge # two sorted arrays # with O(1) extra space. # Merge ar1[] and ar2[] # with O(1) extra space def merge(ar1, ar2, m, n): # Iterate through all # elements of ar2[] starting from # the last element for i in range (n - 1 , - 1 , - 1 ): # Find the smallest element # greater than ar2[i]. Move all # elements one position ahead # till the smallest greater # element is not found last = ar1[m - 1 ] j = m - 2 while (j > = 0 and ar1[j] > ar2[i]): ar1[j + 1 ] = ar1[j] j - = 1 # If there was a greater element if (j ! = m - 2 or last > ar2[i]): ar1[j + 1 ] = ar2[i] ar2[i] = last # Driver program ar1 = [ 1 , 5 , 9 , 10 , 15 , 20 ] ar2 = [ 2 , 3 , 8 , 13 ] m = len (ar1) n = len (ar2) merge(ar1, ar2, m, n) print ( "After Merging First Array:" , end = "") for i in range (m): print (ar1[i] , " " , end = "") print ( "Second Array: " , end = "") for i in range (n): print (ar2[i] , " " , end = "") # This code is contributed # by Anant Agarwal. |
C#
// C# program program to merge two // sorted arrays with O(1) extra space. using System; // Java program program to merge two // sorted arrays with O(1) extra space. public class Test { static int []arr1 = new int []{1, 5, 9, 10, 15, 20}; static int []arr2 = new int []{2, 3, 8, 13}; static void merge( int m, int n) { // Iterate through all elements of ar2[] starting from // the last element for ( int i=n-1; i>=0; i--) { /* Find the smallest element greater than ar2[i]. Move all elements one position ahead till the smallest greater element is not found */ int j, last = arr1[m-1]; for (j=m-2; j >= 0 && arr1[j] > arr2[i]; j--) arr1[j+1] = arr1[j]; // If there was a greater element if (j != m-2 || last > arr2[i]) { arr1[j+1] = arr2[i]; arr2[i] = last; } } } // Driver method to test the above function public static void Main() { merge(arr1.Length,arr2.Length); Console.Write( "After Merging First Array: " ); for ( int i =0; i< arr1.Length;i++){ Console.Write(arr1[i]+ " " ); } Console.Write( "Second Array: " ); for ( int i =0; i< arr2.Length;i++){ Console.Write(arr2[i]+ " " ); } } } /*This code is contributed by 29AjayKumar*/ |
PHP
<?php // PHP program to merge two sorted arrays with O(1) extra space. // Merge ar1[] and ar2[] with O(1) extra space function merge(& $ar1 , & $ar2 , $m , $n ) { // Iterate through all elements of ar2[] starting from // the last element for ( $i = $n -1; $i >= 0; $i --) { /* Find the smallest element greater than ar2[i]. Move all elements one position ahead till the smallest greater element is not found */ $last = $ar1 [ $m -1]; for ( $j = $m -2; $j >= 0 && $ar1 [ $j ] > $ar2 [ $i ]; $j --) $ar1 [ $j +1] = $ar1 [ $j ]; // If there was a greater element if ( $j != $m -2 || $last > $ar2 [ $i ]) { $ar1 [ $j +1] = $ar2 [ $i ]; $ar2 [ $i ] = $last ; } } } // Driver program $ar1 = array (1, 5, 9, 10, 15, 20); $ar2 = array (2, 3, 8, 13); $m = sizeof( $ar1 )/sizeof( $ar1 [0]); $n = sizeof( $ar2 )/sizeof( $ar2 [0]); merge( $ar1 , $ar2 , $m , $n ); echo "After Merging First Array: " ; for ( $i =0; $i < $m ; $i ++) echo $ar1 [ $i ] . " " ; echo "Second Array: " ; for ( $i =0; $i < $n ; $i ++) echo $ar2 [ $i ] . " " ; return 0; ?> |
Javascript
<script> // Javascript program program to merge two // sorted arrays with O(1) extra space. let arr1=[1, 5, 9, 10, 15, 20]; let arr2=[2, 3, 8, 13]; function merge(m,n) { // Iterate through all elements of ar2[] starting from // the last element for (let i=n-1; i>=0; i--) { /* Find the smallest element greater than ar2[i]. Move all elements one position ahead till the smallest greater element is not found */ let j, last = arr1[m-1]; for (j=m-2; j >= 0 && arr1[j] > arr2[i]; j--) arr1[j+1] = arr1[j]; // If there was a greater element if (j != m-2 || last > arr2[i]) { arr1[j+1] = arr2[i]; arr2[i] = last; } } } // Driver method to test the above function merge(arr1.length,arr2.length); document.write( "After Merging <br>First Array: " ); for (let i=0;i<arr1.length;i++) { document.write(arr1[i]+ " " ); } document.write( "<br>Second Array: " ); for (let i=0;i<arr2.length;i++) { document.write(arr2[i]+ " " ); } // This code is contributed by avanitrachhadiya2155 </script> |
输出:
After Merging First Array: 1 2 3 5 8 9 Second Array: 10 13 15 20
时间复杂性: 代码/算法的最坏情况时间复杂度为O(m*n)。最坏的情况发生在ar1[]的所有元素大于ar2[]的所有元素时。
插图:
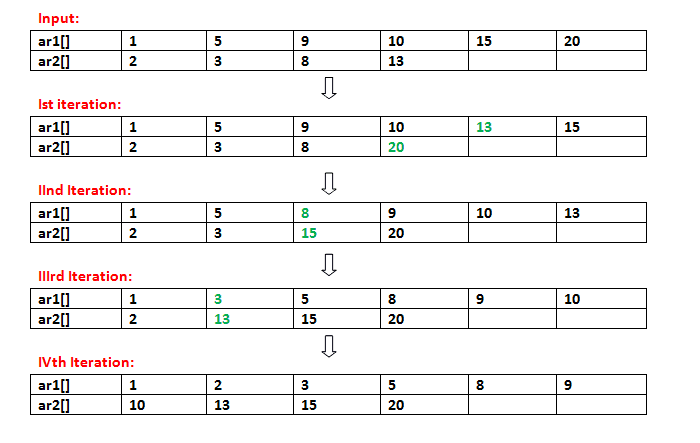
ar1[]={1,5,9,10,15,20}; ar2[]={2,3,8, 13 }; 第一次迭代后: ar1[]={1,5,9,10,13,15}; ar2[]={2,3, 8. , 20}; //20从ar1[]移动到ar2[] //ar2[]中的13插入ar1[] 第二次迭代后: ar1[]={1,5,8,9,10,13}; ar2[]={2, 3. , 15, 20}; //15从ar1[]移动到ar2[] //ar2[]中的8插入ar1[] 第三次迭代后: ar1[]={1,3,5,8,9,10}; ar2[]={ 2. , 13, 15, 20}; //13从ar1[]移动到ar2[] //ar2[]中的3插入ar1[] 第四次迭代后: ar1[]={1,2,3,5,8,9}; ar2[]={10,13,15,20}; //10从ar1[]移动到ar2[] //ar2[]中的2插入到ar1[] —!>
方法2:
通过观察并行遍历两个排序数组时,如果我们遇到第j个第二数组元素小于第i个第一数组元素,则需要包含第j个元素并替换第一数组中的某些第k个元素,从而进一步优化解决方案。这一观察结果有助于我们实现以下算法
算法
1) Initialize i,j,k as 0,0,n-1 where n is size of arr1 2) Iterate through every element of arr1 and arr2 using two pointers i and j respectively if arr1[i] is less than arr2[j] increment i else swap the arr2[j] and arr1[k] increment j and decrement k3) Sort both arr1 and arr2
下面是上述算法的实现
C++
// CPP program for the above approach #include <bits/stdc++.h> using namespace std; // Function to merge two arrays void merge( int arr1[], int arr2[], int n, int m) { int i = 0, j = 0, k = n - 1; // Until i less than equal to k // or j is less than m while (i <= k && j < m) { if (arr1[i] < arr2[j]) i++; else { swap(arr2[j++], arr1[k--]); } } // Sort first array sort(arr1, arr1 + n); // Sort second array sort(arr2, arr2 + m); } // Driver Code int main() { int ar1[] = { 1, 5, 9, 10, 15, 20 }; int ar2[] = { 2, 3, 8, 13 }; int m = sizeof (ar1) / sizeof (ar1[0]); int n = sizeof (ar2) / sizeof (ar2[0]); merge(ar1, ar2, m, n); cout << "After Merging First Array: " ; for ( int i = 0; i < m; i++) cout << ar1[i] << " " ; cout << "Second Array: " ; for ( int i = 0; i < n; i++) cout << ar2[i] << " " ; return 0; } |
JAVA
// Java program for the above approach import java.util.Arrays; import java.util.Collections; class GFG { static int arr1[] = new int [] { 1 , 5 , 9 , 10 , 15 , 20 }; static int arr2[] = new int [] { 2 , 3 , 8 , 13 }; // Function to merge two arrays static void merge( int m, int n) { int i = 0 , j = 0 , k = m - 1 ; while (i <= k && j < n) { if (arr1[i] < arr2[j]) i++; else { int temp = arr2[j]; arr2[j] = arr1[k]; arr1[k] = temp; j++; k--; } } Arrays.sort(arr1); Arrays.sort(arr2); } public static void main(String[] args) { merge(arr1.length, arr2.length); System.out.print( "After Merging First Array: " ); System.out.println(Arrays.toString(arr1)); System.out.print( "Second Array: " ); System.out.println(Arrays.toString(arr2)); } } |
Python3
# Python program for the above approach arr1 = [ 1 , 5 , 9 , 10 , 15 , 20 ]; arr2 = [ 2 , 3 , 8 , 13 ]; # Function to merge two arrays def merge(m, n): i = 0 ; j = 0 ; k = n - 1 ; while (i < = k and j < m): if (arr1[i] < arr2[j]): i + = 1 ; else : temp = arr2[j]; arr2[j] = arr1[k]; arr1[k] = temp; j + = 1 ; k - = 1 ; arr1.sort(); arr2.sort(); # Driver code if __name__ = = '__main__' : merge( len (arr1), len (arr2)); print ( "After Merging First Array: " ); print ( ',' .join( str (x) for x in arr1)); print ( "Second Array: " ); print ( ',' .join( str (x) for x in arr2)); # This code is contributed by gauravrajput1 |
C#
// C# program for the above approach using System; public class GFG { static int []arr1 ={ 1, 5, 9, 10, 15, 20 }; static int []arr2 = { 2, 3, 8, 13 }; // Function to merge two arrays static void merge( int m, int n) { int i = 0, j = 0, k = n - 1; while (i <= k && j < m) { if (arr1[i] < arr2[j]) i++; else { int temp = arr2[j]; arr2[j] = arr1[k]; arr1[k] = temp; j++; k--; } } Array.Sort(arr1); Array.Sort(arr2); } public static void Main(String[] args) { merge(arr1.Length, arr2.Length); Console.Write( "After Merging First Array: " ); foreach ( int i in arr1){ Console.Write(i+ " " ); } Console.Write( "Second Array: " ); foreach ( int i in arr2){ Console.Write(i+ " " ); } } } // This code is contributed by gauravrajput1 |
Javascript
<script> // javascript program for the above approach var arr1 = [ 1, 5, 9, 10, 15, 20 ]; var arr2 = [ 2, 3, 8, 13 ]; // Function to merge two arrays function merge(m , n) { var i = 0, j = 0, k = n - 1; while (i <= k && j < m) { if (arr1[i] < arr2[j]) i++; else { var temp = arr2[j]; arr2[j] = arr1[k]; arr1[k] = temp; j++; k--; } } arr1.sort((a,b)=>a-b); arr2.sort((a,b)=>a-b); } merge(arr1.length, arr2.length); document.write( "After Merging <br/>First Array:<br/> " ); for ( var a of arr1) document.write(a+ " " ); document.write( "<br/>Second Array: <br/> " ); for ( var a of arr2) document.write(a+ " " ); // This code is contributed by gauravrajput1 </script> |
After Merging First Array: 1 2 3 5 8 9 Second Array: 10 13 15 20
复杂性:
时间复杂度:在while循环中遍历数组时,最坏情况下的时间复杂度为O(n+m),排序为O(nlog(n)+mlog(m))。所以代码的总体时间复杂度变成O((n+m)log(n+m))。
空间复杂度:由于函数不使用任何额外的数组进行任何操作,因此空间复杂度为O(1)。
方法3:
算法:
1) Initialize i with 02) Iterate while loop until last element of array 1 is greater than first element of array 2 if arr1[i] greater than first element of arr2 swap arr1[i] with arr2[0] sort arr2 incrementing i
C++
#include<iostream> #include<bits/stdc++.h> using namespace std; void merge( int arr1[], int arr2[], int n, int m) { int i=0; // while loop till last element of array 1(sorted) is greater than // first element of array 2(sorted) while (arr1[n-1]>arr2[0]) { if (arr1[i]>arr2[0]) { // swap arr1[i] with first element // of arr2 and sorting the updated // arr2(arr1 is already sorted) swap(arr1[i],arr2[0]); sort(arr2,arr2+m); } i++; } } int main() { int ar1[] = { 1, 5, 9, 10, 15, 20 }; int ar2[] = { 2, 3, 8, 13 }; int m = sizeof (ar1) / sizeof (ar1[0]); int n = sizeof (ar2) / sizeof (ar2[0]); merge(ar1, ar2, m, n); cout << "After Merging First Array: " ; for ( int i = 0; i < m; i++) cout << ar1[i] << " " ; cout << "Second Array: " ; for ( int i = 0; i < n; i++) cout << ar2[i] << " " ; return 0; } |
JAVA
import java.io.*; import java.util.Arrays; import java.util.Collections; class GFG{ static int arr1[] = new int []{ 1 , 5 , 9 , 10 , 15 , 20 }; static int arr2[] = new int []{ 2 , 3 , 8 , 13 }; static void merge( int n, int m) { int i = 0 ; int temp = 0 ; // While loop till last element // of array 1(sorted) // is greater than first element // of array 2(sorted) while (arr1[n - 1 ] > arr2[ 0 ]) { if (arr1[i] > arr2[ 0 ]) { // Swap arr1[i] with first element // of arr2 and sorting the updated // arr2(arr1 is already sorted) // swap(arr1[i],arr2[0]); temp = arr1[i]; arr1[i] = arr2[ 0 ]; arr2[ 0 ] = temp; Arrays.sort(arr2); } i++; } } // Driver code public static void main(String[] args) { merge(arr1.length, arr2.length); System.out.print( "After Merging First Array: " ); System.out.println(Arrays.toString(arr1)); System.out.print( "Second Array: " ); System.out.println(Arrays.toString(arr2)); } } // This code is contributed by Aakash Tiwari(nighteagle) |
Python3
arr1 = [ 1 , 5 , 9 , 10 , 15 , 20 ]; arr2 = [ 2 , 3 , 8 , 13 ]; def merge(n, m): i = 0 ; temp = 0 ; # While loop till last element # of array 1(sorted) # is greater than first element # of array 2(sorted) while (arr1[n - 1 ] > arr2[ 0 ]): if (arr1[i] > arr2[ 0 ]): # Swap arr1[i] with first element # of arr2 and sorting the updated # arr2(arr1 is already sorted) # swap(arr1[i],arr2[0]); temp = arr1[i]; arr1[i] = arr2[ 0 ]; arr2[ 0 ] = temp; arr2.sort(); i + = 1 ; # Driver code if __name__ = = '__main__' : merge( len (arr1), len (arr2)); print ( "After Merging First Array: " ); print ((arr1)); print ( "Second Array: " ); print ((arr2)); # This code contributed by gauravrajput1 |
C#
using System; public class GFG { static int []arr1 = new int [] { 1, 5, 9, 10, 15, 20 }; static int []arr2 = new int [] { 2, 3, 8, 13 }; static void merge( int n, int m) { int i = 0; int temp = 0; // While loop till last element // of array 1(sorted) // is greater than first element // of array 2(sorted) while (arr1[n - 1] > arr2[0]) { if (arr1[i] > arr2[0]) { // Swap arr1[i] with first element // of arr2 and sorting the updated // arr2(arr1 is already sorted) // swap(arr1[i],arr2[0]); temp = arr1[i]; arr1[i] = arr2[0]; arr2[0] = temp; Array.Sort(arr2); } i++; } } // Driver code public static void Main(String[] args) { merge(arr1.Length, arr2.Length); Console.Write( "After Merging First Array: " ); foreach ( int i in arr1) Console.Write(i+ " " ); Console.Write( "Second Array: " ); foreach ( int i in arr2) Console.Write(i+ " " ); } } // This code is contributed by gauravrajput1 |
Javascript
<script> var arr1 = [1, 5, 9, 10, 15, 20 ]; var arr2 =[2, 3, 8, 13 ]; function merge(n , m) { var i = 0; var temp = 0; // While loop till last element // of array 1(sorted) // is greater than first element // of array 2(sorted) while (arr1[n - 1] > arr2[0]) { if (arr1[i] > arr2[0]) { // Swap arr1[i] with first element // of arr2 and sorting the updated // arr2(arr1 is already sorted) // swap(arr1[i],arr2[0]); temp = arr1[i]; arr1[i] = arr2[0]; arr2[0] = temp; arr2.sort((a,b)=>a-b); } i++; } } // Driver code merge(arr1.length, arr2.length); document.write( "After Merging <br>First Array: " ); document.write(arr1.toString()); document.write( "<br>Second Array: " ); document.write(arr2.toString()); // This code is contributed by umadevi9616 </script> |
After Merging First Array: 1 2 3 5 8 9 Second Array: 10 13 15 20
方法4: 让较短数组的长度为“m”,较大数组的长度为“n”
第一步 :选择较短的数组并找到 指数 应该在哪个位置进行分区。与此类似 https://www.geeksforgeeks.org/median-of-two-sorted-arrays-of-different-sizes/
第一步 :在中位数处对较短的数组进行分区 (l1) .
第二步 :选择第一个 n-l1 第二个数组中的元素。
![图片[2]-用O(1)个额外空间合并两个已排序数组-yiteyi-C++库](https://www.yiteyi.com/wp-content/uploads/geeks/20210611/geeks_mtsa-300x90.png)
第三步 :比较边框元素,即。
如果 l1
否则如果 l1>r2 我们必须在左边的子数组中搜索
否则我们必须在正确的子数组中搜索
注意:此步骤将在较短的数组中存储所有最小的元素。
第二步 :将所有元素直接交换到 索引(一) 使用第一个 n-i 较大数组的元素。
第三步 :对两个数组进行排序。
::::: 如果 len(arr1)>len(arr2) 所有最小的元素都存储在 啊2 所以我们必须把所有元素移入 啊 因为我们得打印 啊 第一
第四步 :旋转较大的阵列 (1)米 时间是逆时针的。
第五步 :交换第一个 M 两个数组的元素。
C++
#include <bits/stdc++.h> using namespace std; void swap( int & a, int & b) { int temp = a; a = b; b = temp; } void rotate( int a[], int n, int idx) { int i; for (i = 0; i < idx / 2; i++) swap(a[i], a[idx - 1 - i]); for (i = idx; i < (n + idx) / 2; i++) swap(a[i], a[n - 1 - (i - idx)]); for (i = 0; i < n / 2; i++) swap(a[i], a[n - 1 - i]); } void sol( int a1[], int a2[], int n, int m) { int l = 0, h = n - 1, idx = 0; //--------------------------------------------------------- while (l <= h) { // select the median of the remaining subarray int c1 = (l + h) / 2; // select the first elements from the larger array // equal to the size of remaining portion to the // right of the smaller array int c2 = n - c1 - 1; int l1 = a1[c1]; int l2 = a2[c2 - 1]; int r1 = c1 == n - 1 ? INT_MAX : a1[c1 + 1]; int r2 = c2 == m ? INT_MAX : a2[c2]; // compare the border elements and check for the // target index if (l1 > r2) { h = c1 - 1; if (h == -1) idx = 0; } else if (l2 > r1) { l = c1 + 1; if (l == n - 1) idx = n; } else { idx = c1 + 1; break ; } } for ( int i = idx; i < n; i++) swap(a1[i], a2[i - idx]); sort(a1, a1 + n); sort(a2, a2 + m); } void merge( int arr1[], int arr2[], int n, int m) { // code here if (n > m) { sol(arr2, arr1, m, n); rotate(arr1, n, n - m); for ( int i = 0; i < m; i++) swap(arr2[i], arr1[i]); } else { sol(arr1, arr2, n, m); } } int main() { int ar1[] = { 1, 5, 9, 10, 15, 20 }; int ar2[] = { 2, 3, 8, 13 }; int m = sizeof (ar1) / sizeof (ar1[0]); int n = sizeof (ar2) / sizeof (ar2[0]); merge(ar1, ar2, m, n); cout << "After Merging First Array: " ; for ( int i = 0; i < m; i++) cout << ar1[i] << " " ; cout << "Second Array: " ; for ( int i = 0; i < n; i++) cout << ar2[i] << " " ; return 0; } |
JAVA
// Java program for the above approach import java.util.*; class GFG { static void swap( int a, int b) { int temp = a; a = b; b = temp; } static void rotate( int a[], int n, int idx) { int i; for (i = 0 ; i < idx / 2 ; i++) swap(a[i], a[idx - 1 - i]); for (i = idx; i < (n + idx) / 2 ; i++) swap(a[i], a[n - 1 - (i - idx)]); for (i = 0 ; i < n / 2 ; i++) swap(a[i], a[n - 1 - i]); } static void sol( int a1[], int a2[], int n, int m) { int l = 0 , h = n - 1 , idx = 0 ; //--------------------------------------------------------- while (l <= h) { // select the median of the remaining subarray int c1 = ( int )(l + h) / 2 ; // select the first elements from the larger array // equal to the size of remaining portion to the // right of the smaller array int c2 = n - c1 - 1 ; int l1 = a1[c1]; int l2 = a2[c2 - 1 ]; int r1 = (c1 == n - 1 ) ? Integer.MAX_VALUE : a1[c1 + 1 ]; int r2 = (c2 == m) ? Integer.MAX_VALUE : a2[c2]; // compare the border elements and check for the // target index if (l1 > r2) { h = c1 - 1 ; if (h == - 1 ) idx = 0 ; } else if (l2 > r1) { l = c1 + 1 ; if (l == n - 1 ) idx = n; } else { idx = c1 + 1 ; break ; } } for ( int i = idx; i < n; i++) swap(a1[i], a2[i - idx]); Arrays.sort(a1); Arrays.sort(a2); } static void merge( int arr1[], int arr2[], int n, int m) { // code here if (n > m) { sol(arr2, arr1, m, n); rotate(arr1, n, n - m); for ( int i = 0 ; i < m; i++) swap(arr2[i], arr1[i]); } else { sol(arr1, arr2, n, m); } } // Driver Code public static void main (String[] args) { int ar1[] = { 1 , 5 , 9 , 10 , 15 , 20 }; int ar2[] = { 2 , 3 , 8 , 13 }; int m = ar1.length; int n = ar2.length; merge(ar1, ar2, m, n); System.out.print( "After Merging First Array: " ); for ( int i = 0 ; i < m; i++) System.out.print(ar1[i] + " " ); System.out.print( "Second Array: " ); for ( int i = 0 ; i < n; i++) System.out.print(ar2[i] + " " ); } } // This code is contributed by sanjoy_62. |
Python3
# Python program to merge # two sorted arrays # with O(1) extra space. # Merge ar1[] and ar2[] # with O(1) extra space def rotate(a, n, idx): for i in range (( int )(idx / 2 )): a[i], a[idx - 1 - i] = a[idx - 1 - i], a[i] for i in range (idx, ( int )((n + idx) / 2 )): a[i], a[n - 1 - (i - idx)] = a[n - 1 - (i - idx)], a[i] for i in range (( int )(n / 2 )): a[i], a[n - 1 - i] = a[n - 1 - i], a[i] def sol(a1, a2, n, m): l = 0 h = n - 1 idx = 0 while (l < = h): c1 = ( int )((l + h) / 2 ) c2 = n - c1 - 1 l1 = a1[c1] l2 = a2[c2 - 1 ] r1 = sys.maxint if c1 = = n - 1 else a1[c1 + 1 ] r2 = sys.maxint if c2 = = m else a2[c2] if l1 > r2: h = c1 - 1 if h = = - 1 : idx = 0 elif l2 > r1: l = c1 + 1 if l = = n - 1 : idx = n else : idx = c1 + 1 break for i in range (idx, n): a1[i], a2[i - idx] = a2[i - idx], a1[i] a1.sort() a2.sort() def merge(a1, a2, n, m): if n > m: sol(a2, a1, m, n) rotate(a1, n, n - m) for i in range (m): a1[i], a2[i] = a2[i], a1[i] else : sol(a1, a2, n, m) # Driver program ar1 = [ 1 , 5 , 9 , 10 , 15 , 20 ] ar2 = [ 2 , 3 , 8 , 13 ] m = len (ar1) n = len (ar2) merge(ar1, ar2, m, n) print ( "After Merging First Array:" , end = "") for i in range (m): print (ar1[i], " " , end = "") print ( "Second Array: " , end = "") for i in range (n): print (ar2[i], " " , end = "") # This code is contributed # by Aditya Anand. |
C#
// C# program for the above approach using System; using System.Collections.Generic; public class GFG { static void swap( int a, int b) { int temp = a; a = b; b = temp; } static void rotate( int []a, int n, int idx) { int i; for (i = 0; i < idx / 2; i++) swap(a[i], a[idx - 1 - i]); for (i = idx; i < (n + idx) / 2; i++) swap(a[i], a[n - 1 - (i - idx)]); for (i = 0; i < n / 2; i++) swap(a[i], a[n - 1 - i]); } static void sol( int []a1, int []a2, int n, int m) { int l = 0, h = n - 1, idx = 0; // --------------------------------------------------------- while (l <= h) { // select the median of the remaining subarray int c1 = ( int ) (l + h) / 2; // select the first elements from the larger array // equal to the size of remaining portion to the // right of the smaller array int c2 = n - c1 - 1; int l1 = a1[c1]; int l2 = a2[c2 - 1]; int r1 = (c1 == n - 1) ? int .MaxValue : a1[c1 + 1]; int r2 = (c2 == m) ? int .MaxValue : a2[c2]; // compare the border elements and check for the // target index if (l1 > r2) { h = c1 - 1; if (h == -1) idx = 0; } else if (l2 > r1) { l = c1 + 1; if (l == n - 1) idx = n; } else { idx = c1 + 1; break ; } } for ( int i = idx; i < n; i++) swap(a1[i], a2[i - idx]); Array.Sort(a1); Array.Sort(a2); } static void merge( int []arr1, int []arr2, int n, int m) { // code here if (n > m) { sol(arr2, arr1, m, n); rotate(arr1, n, n - m); for ( int i = 0; i < m; i++) swap(arr2[i], arr1[i]); } else { sol(arr1, arr2, n, m); } } // Driver Code public static void Main(String[] args) { int []ar1 = { 1, 5, 9, 10, 15, 20 }; int []ar2 = { 2, 3, 8, 13 }; int m = ar1.Length; int n = ar2.Length; merge(ar1, ar2, m, n); Console.Write( "After Merging First Array: " ); for ( int i = 0; i < m; i++) Console.Write(ar1[i] + " " ); Console.Write( "Second Array: " ); for ( int i = 0; i < n; i++) Console.Write(ar2[i] + " " ); } } // This code contributed by gauravrajput1 |
Javascript
<script> // javascript program for the above approach function swap(a , b) { var temp = a; a = b; b = temp; } function rotate(a , n , idx) { var i; for (i = 0; i < idx / 2; i++) { var temp =a[i] a[i]= a[idx - 1 - i]; a[idx - 1 - i] = temp; } for (i = idx; i < (n + idx) / 2; i++) { var temp =a[i] a[i]= a[n - 1 - (i - idx)]; a[n - 1 - (i - idx)] = temp; } for (i = 0; i < n / 2; i++) { var temp =a[i] a[i]= a[n - 1 - i]; a[n - 1 - i] = temp; } } function sol(a1 , a2 , n , m) { var l = 0, h = n - 1, idx = 0; // --------------------------------------------------------- while (l <= h) { // select the median of the remaining subarray var c1 = parseInt( (l + h) / 2); // select the first elements from the larger array // equal to the size of remaining portion to the // right of the smaller array var c2 = n - c1 - 1; var l1 = a1[c1]; var l2 = a2[c2 - 1]; var r1 = (c1 == n - 1) ? Number.MAX_VALUE : a1[c1 + 1]; var r2 = (c2 == m) ? Number.MAX_VALUE : a2[c2]; // compare the border elements and check for the // target index if (l1 > r2) { h = c1 - 1; if (h == -1) idx = 0; } else if (l2 > r1) { l = c1 + 1; if (l == n - 1) idx = n; } else { idx = c1 + 1; break ; } } for (i = idx; i < n; i++) { var temp =a1[i] a1[i]= a2[i - idx]; a2[i - idx] = temp; } a1.sort((a,b)=>a-b); a2.sort((a,b)=>a-b); } function merge(arr1 , arr2 , n , m) { // code here if (n > m) { sol(arr2, arr1, m, n); rotate(arr1, n, n - m); for (i = 0; i < m; i++) { var temp =arr2[i] arr2[i]= arr1[i]; arr1[i] = temp; } } else { sol(arr1, arr2, n, m); } } // Driver Code var ar1 = [ 1, 5, 9, 10, 15, 20 ]; var ar2 = [ 2, 3, 8, 13 ]; var m = ar1.length; var n = ar2.length; merge(ar1, ar2, m, n); document.write( "After Merging First Array: " ); for (i = 0; i < m; i++) document.write(ar1[i] + " " ); document.write( "Second Array: " ); for (i = 0; i < n; i++) document.write(ar2[i] + " " ); // This code is contributed by gauravrajput1 </script> |
After Merging First Array: 1 2 3 5 8 9 Second Array: 10 13 15 20
时间复杂性: O(最小值(nlogn、mlogm))
方法5[插入排序与同步合并]
方法:
1.通过始终与列表2的开头/第一个进行比较,并在需要时交换,对列表1进行排序 2.在每次头部/第一次交换后,将交换的元素插入列表2中的正确位置,最终将在末尾对列表2进行排序。
对于列表1中的每个交换项,在列表2中执行插入排序以找到其正确位置,以便在对列表1进行排序时,也对列表2进行排序。
C++
#include <bits/stdc++.h> using namespace std; void merge( int arr1[], int arr2[], int n, int m) { // two pointer to iterate int i = 0; int j = 0; while (i < n && j < m) { // if arr1[i] <= arr2[j] then both array is already // sorted if (arr1[i] <= arr2[j]) { i++; } else if (arr1[i] > arr2[j]) { // if arr1[i]>arr2[j] then first we swap both // element so that arr1[i] become smaller means // arr1[] become sorted then we check that // arr2[j] is smaller then all other element in // right side of arr2[j] if arr2[] is not sorted // then we linearly do sorting // means while adjacent element are less than // new arr2[j] we do sorting like by changing // position of element by shifting one position // toward left swap(arr1[i], arr2[j]); i++; if (j < m - 1 && arr2[j + 1] < arr2[j]) { int temp = arr2[j]; int tempj = j + 1; while (arr2[tempj] < temp && tempj < m) { arr2[tempj - 1] = arr2[tempj]; tempj++; } arr2[tempj - 1] = temp; } } } } int main() { int ar1[] = { 1, 5, 9, 10, 15, 20 }; int ar2[] = { 2, 3, 8, 13 }; int m = sizeof (ar1) / sizeof (ar1[0]); int n = sizeof (ar2) / sizeof (ar2[0]); merge(ar1, ar2, m, n); cout << "After Merging First Array: " ; for ( int i = 0; i < m; i++) cout << ar1[i] << " " ; cout << "Second Array: " ; for ( int i = 0; i < n; i++) cout << ar2[i] << " " ; return 0; } |
JAVA
import java.util.*; class GFG{ static void merge( int arr1[], int arr2[], int n, int m) { // two pointer to iterate int i = 0 ; int j = 0 ; while (i < n && j < m) { // if arr1[i] <= arr2[j] then both array is already // sorted if (arr1[i] <= arr2[j]) { i++; } else if (arr1[i] > arr2[j]) { // if arr1[i]>arr2[j] then first we swap both // element so that arr1[i] become smaller means // arr1[] become sorted then we check that // arr2[j] is smaller then all other element in // right side of arr2[j] if arr2[] is not sorted // then we linearly do sorting // means while adjacent element are less than // new arr2[j] we do sorting like by changing // position of element by shifting one position // toward left int t = arr1[i]; arr1[i] = arr2[j]; arr2[j] = t; i++; if (j < m - 1 && arr2[j + 1 ] < arr2[j]) { int temp = arr2[j]; int tempj = j + 1 ; while (tempj<m && arr2[tempj] < temp && tempj < m) { arr2[tempj - 1 ] = arr2[tempj]; tempj++; } arr2[tempj - 1 ] = temp; } } } } public static void main(String[] args) { int ar1[] = { 1 , 5 , 9 , 10 , 15 , 20 }; int ar2[] = { 2 , 3 , 8 , 13 }; int m = ar1.length; int n =ar2.length; merge(ar1, ar2, m, n); System.out.print( "After Merging First Array: " ); for ( int i = 0 ; i < m; i++) System.out.print(ar1[i]+ " " ); System.out.print( "Second Array: " ); for ( int i = 0 ; i < n; i++) System.out.print(ar2[i]+ " " ); } } // This code is contributed by gauravrajput1 |
Python3
# code contributed by mahee96 # "Insertion sort of list 2 with swaps from list 1" # # swap elements to get list 1 correctly, meanwhile # place the swapped item in correct position of list 2 # eventually list 2 is also sorted # Time = O(m*n) or O(n*m) # AUX = O(1) def merge(arr1, arr2): x = arr1; y = arr2 end = len (arr1) i = 0 while (i < end): # O(m) or O(n) if (x[i] > y[ 0 ]): swap(x,y,i, 0 ) insert(y, 0 ) # O(n) or O(m) number of shifts i + = 1 # O(n): def insert(y, i): orig = y[i] i + = 1 while (i< len (y) and y[i]<orig): y[i - 1 ] = y[i] i + = 1 y[i - 1 ] = orig def swap(x,y,i,j): temp = x[i] x[i] = y[j] y[j] = temp def test(): c1 = [ 2 , 3 , 8 , 13 ] c2 = [ 1 , 5 , 9 , 10 , 15 , 20 ] for _ in range ( 2 ): merge(c1,c2) print (c1,c2) c1, c2 = c2, c1 test() |
C#
using System; public class GFG { static void merge( int []arr1, int []arr2, int n, int m) { // two pointer to iterate int i = 0; int j = 0; while (i < n && j < m) { // if arr1[i] <= arr2[j] then both array is already // sorted if (arr1[i] <= arr2[j]) { i++; } else if (arr1[i] > arr2[j]) { // if arr1[i]>arr2[j] then first we swap both // element so that arr1[i] become smaller means // arr1[] become sorted then we check that // arr2[j] is smaller then all other element in // right side of arr2[j] if arr2[] is not sorted // then we linearly do sorting // means while adjacent element are less than // new arr2[j] we do sorting like by changing // position of element by shifting one position // toward left int t = arr1[i]; arr1[i] = arr2[j]; arr2[j] = t; i++; if (j < m - 1 && arr2[j + 1] < arr2[j]) { int temp = arr2[j]; int tempj = j + 1; while (tempj < m && arr2[tempj] < temp && tempj < m) { arr2[tempj - 1] = arr2[tempj]; tempj++; } arr2[tempj - 1] = temp; } } } } public static void Main(String[] args) { int []ar1 = { 1, 5, 9, 10, 15, 20 }; int []ar2 = { 2, 3, 8, 13 }; int m = ar1.Length; int n = ar2.Length; merge(ar1, ar2, m, n); Console.Write( "After Merging First Array: " ); for ( int i = 0; i < m; i++) Console.Write(ar1[i] + " " ); Console.Write( "Second Array: " ); for ( int i = 0; i < n; i++) Console.Write(ar2[i] + " " ); } } // This code is contributed by gauravrajput1 |
Javascript
<script> function merge(arr1 , arr2 , n , m) { // two pointer to iterate var i = 0; var j = 0; while (i < n && j < m) { // if arr1[i] <= arr2[j] then both array is already // sorted if (arr1[i] <= arr2[j]) { i++; } else if (arr1[i] > arr2[j]) { // if arr1[i]>arr2[j] then first we swap both // element so that arr1[i] become smaller means // arr1 become sorted then we check that // arr2[j] is smaller then all other element in // right side of arr2[j] if arr2 is not sorted // then we linearly do sorting // means while adjacent element are less than // new arr2[j] we do sorting like by changing // position of element by shifting one position // toward left var t = arr1[i]; arr1[i] = arr2[j]; arr2[j] = t; i++; if (j < m - 1 && arr2[j + 1] < arr2[j]) { var temp = arr2[j]; var tempj = j + 1; while (tempj < m && arr2[tempj] < temp && tempj < m) { arr2[tempj - 1] = arr2[tempj]; tempj++; } arr2[tempj - 1] = temp; } } } } var ar1 = [ 1, 5, 9, 10, 15, 20 ]; var ar2 = [ 2, 3, 8, 13 ]; var m = ar1.length; var n = ar2.length; merge(ar1, ar2, m, n); document.write( "After Merging <br/>First Array: <br/>" ); for (i = 0; i < m; i++) document.write(ar1[i] + " " ); document.write( "<br/>Second Array: <br/>" ); for (i = 0; i < n; i++) document.write(ar2[i] + " " ); // This code contributed by gauravrajput1 </script> |
After Merging First Array: 1 2 3 5 8 9 Second Array: 10 13 15 20
时间复杂性: O(m*n)列表1遍历和列表2插入 辅助空间: O(1) 如果m=n:Time=O(n^2)插入排序复杂性
相关文章: 合并两个排序的数组 合并k个排序数组|集1 感谢Shubham Chauhan提出的第一种解决方案,以及Himanshu Kaushik提出的第二种解决方案。如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



