我们知道前n个自然数的平方和是 ![]() .
.
null
如何计算前n个偶数自然数的平方和? 我们需要计算2 2. + 4 2. + 6 2. + …. + (2n) 2.
EvenSum = 22 + 42 + 62 + .... + (2n)2
= 4 x (12 + 22 + 32 + .... + (n)2)
= 4n(n+1)(2n+1)/6
= 2n(n+1)(2n+1)/3
例子:
Sum of squares of first 3 even numbers =
2n(n+1)(2n+1)/3
= 2*3(3+1)(2*3+1)/3
= 56
22 + 42 + 62 = 4 + 16 + 36 = 56
如何计算前n个奇数自然数的平方和? 我们需要计算1 2. + 3 2. + 5 2. + …. + (2n-1) 2.
OddSum = (Sum of Squares of all 2n numbers) -
(Sum of squares of first n even numbers)
= 2n*(2n+1)*(2*2n + 1)/6 - 2n(n+1)(2n+1)/3
= 2n(2n+1)/6 [4n+1 - 2(n+1)]
= n(2n+1)/3 * (2n-1)
= n(2n+1)(2n-1)/3
例子:
Sum of squares of first 3 odd numbers = n(2n+1)(2n-1)/3
= 3(2*3+1)(2*3-1)/3
= 35
12 + 32 + 52 = 1 + 9 + 25 = 35
如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写评论
© 版权声明
文章版权归作者所有,未经允许请勿转载。
THE END
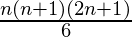


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



