计算理论中的泵引理

有两个泵引理，它们被定义为 1.常规语言，以及 2.上下文无关语言 正则语言的泵引理 对于任何正则语言L，都存在一个整数n，因此对于所有x∈ L与| x |≥ n、 存在u，v，w∈ Σ∗, 这样x=uvw，并且 （1） |紫外线|≤ N （2） |v|≥ 1. （3） 尽管我≥ 0:uv ^我 W∈ L 简单地说，这意味着如果一个字符串v被“抽运”，即如果v被插入任意次数，则合成的字符串仍保留在L中。 泵引理被用来证明语言的不规则性。因此，如果一种语言是正则的，它总是满足泵引理。如果至少有一根由泵送制成的管柱不在L中，那么L肯定不是规则的。 与此相反的情况可能并不总是如此。也就是说，如果泵引理成立，并不意味着语言是正则的。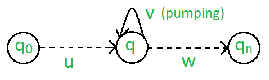

例如，让我们证明我 ₀₁ = {0 ^N 1 ^N |n≥ 0}是不规则的。 假设L是正则的，那么通过抽引理，上述规则就遵循了。 现在，让x∈ L和| x |≥ n、 所以，通过抽运引理，存在u，v，w，使得（1）-（3）成立。 我们证明，对于所有的u，v，w，（1）-（3）都不成立。 如果（1）和（2）保持不变，那么x=0 ^N 1. ^N =uvw带| uv |≤ n和| v |≥ 1. 所以，u=0 ^A. ，v=0 ^B ，w=0 ^C 1. ⁿ 地点：a+b≤ 请注意≥ 1，c≥ 0，a+b+c=n 但是，如果i=0，则（3）失败 紫外线 ⁰ w=uw=0 ^A. 0 ^C 1. ^N = 0 ^a+c 1. ^N ∉ 五十、 从a+c开始≠ N 上下文无关语言（CFL）的泵送引理 CFL的泵送引理表明，对于任何上下文无关的语言L，都有可能找到两个子串，它们可以被“泵送”任意次数，并且仍然是同一种语言。对于它的第四个部分，我们把第二个字符串分成五个部分。 这里，泵引理也被用作证明语言不是CFL的工具。因为，如果任何一个字符串不满足其条件，那么该语言就不是CFL。 因此，如果L是CFL，则存在整数n，因此对于所有x∈ L与| x |≥ n、 存在u，v，w，x，y∈ Σ∗, 这样x=uvwxy，并且 （1） |vwx |≤ N （2） |vx |≥ 1. （3） 尽管我≥ 0:uv ^我 wx ^我 Y∈ L

对于上面的例子，0 ^N 1. ⁿ 是CFL，因为任何管柱都可能是在两个位置泵送的结果，一个为0，另一个为1。 让我们证明，我 ₀₁₂ = {0 ^N 1. ^N 2. ⁿ |n≥ 0}不是上下文无关的。 假设L是上下文无关的，那么通过抽引理，上面给出的规则就遵循了。 现在，让x∈ L和| x |≥ n、 所以，通过抽运引理，存在u，v，w，x，y，使得（1）-（3）成立。 我们证明，对于所有的u，v，w，x，y（1）-（3）都不成立。 如果（1）和（2）保持不变，那么x=0 ^N 1. ^N 2. ^N =uvwxy带| vwx |≤ n和| vx |≥ 1. （1） 告诉我们vwx不同时包含0和2。因此，要么VWX没有0，要么VWX没有2。因此，我们有两个案例需要考虑。 假设vwx没有0。根据（2），vx包含1或2。因此，uwy具有“n”0，uwy要么小于“n”1，要么小于“n”2。 但是（3）告诉我们uwy=uv ⁰ wx ⁰ Y∈ L 所以，uwy的0，1和2的数量相等，这给了我们一个矛盾。vwx没有2号的情况类似，也给我们带来了矛盾。因此L不是上下文无关的。

资料来源：约翰·E·霍普克罗夫特、拉杰夫·莫特瓦尼、杰弗里·D·厄尔曼（2003年）。介绍自动机理论、语言和计算。 本文由 尼鲁帕姆·辛格 . 如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写评论