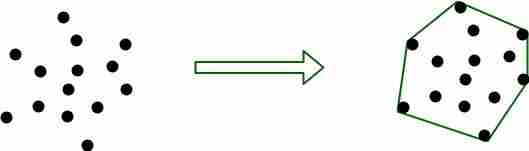
凸壳的快速壳算法-yiteyi-C++库

给定一组点，凸包是包含所有给定点的最小凸多边形。

null

输入是由x和y坐标指定的点的数组。输出是按x坐标升序排列的这组点的凸包。

例子：

Input : points[] = {{0, 3}, {1, 1}, {2, 2}, {4, 4},
                    {0, 0}, {1, 2}, {3, 1}, {3, 3}};
Output :  The points in convex hull are:
          (0, 0) (0, 3) (3, 1) (4, 4)

Input : points[] = {{0, 3}, {1, 1}
Output : Not Possible
There must be at least three points to form a hull.

Input  : points[] = {(0, 0), (0, 4), (-4, 0), (5, 0), 
                     (0, -6), (1, 0)};
Output : (-4, 0), (5, 0), (0, -6), (0, 4)

建议：请在“上解决” 实践 “首先，在讨论解决方案之前。

我们讨论了凸壳问题的以下算法。凸壳|集1（贾维斯算法或换行）凸包|集2（格雷厄姆扫描）

QuickHull算法是一种分而治之的算法，类似于快速排序 .设[0…n-1]为点的输入数组。以下是找到这些点的凸包的步骤。

找到具有最小x坐标的点，比如说，min_x，同样地，找到具有最大x坐标的点，max_x。
把这两点连接起来，比如 L .这条线将把整套设备分成两部分。把这两个部分一个接一个地讲下去。
对于一个零件，找到距离线L最大的点P。P与点min_x，max_x形成一个三角形。很明显，位于这个三角形内的点永远不可能是凸包的一部分。
上述步骤将问题分为两个子问题（递归求解）。现在，连接点P和min_x的线和连接点P和max_x的线是新线，位于三角形外的点是点集。重复第3点，直到线没有剩余的点为止。将该点的端点添加到凸面外壳。

下面是C++实现上述思想。实现使用设置存储点，以便按排序顺序打印点。点被表示为一对 .

                     // C++ program to implement Quick Hull algorithm                   
                     // to find convex hull.                   
                     #include<bits/stdc++.h>                   
                     using                               namespace                               std;                   
                             
                     // iPair is integer pairs                   
                     #define iPair pair<int, int>                   
                             
                     // Stores the result (points of convex hull)                   
                     set<iPair> hull;                   
                             
                     // Returns the side of point p with respect to line                   
                     // joining points p1 and p2.                   
                     int                               findSide(iPair p1, iPair p2, iPair p)                   
                     {                   
                                         int                               val = (p.second - p1.second) * (p2.first - p1.first) -                   
                                         (p2.second - p1.second) * (p.first - p1.first);                   
                             
                                         if                               (val > 0)                   
                                         return                               1;                   
                                         if                               (val < 0)                   
                                         return                               -1;                   
                                         return                               0;                   
                     }                   
                             
                     // returns a value proportional to the distance                   
                     // between the point p and the line joining the                   
                     // points p1 and p2                   
                     int                               lineDist(iPair p1, iPair p2, iPair p)                   
                     {                   
                                         return                               abs                               ((p.second - p1.second) * (p2.first - p1.first) -                   
                                         (p2.second - p1.second) * (p.first - p1.first));                   
                     }                   
                             
                     // End points of line L are p1 and p2.  side can have value                   
                     // 1 or -1 specifying each of the parts made by the line L                   
                     void                               quickHull(iPair a[],                               int                               n, iPair p1, iPair p2,                               int                               side)                   
                     {                   
                                         int                               ind = -1;                   
                                         int                               max_dist = 0;                   
                             
                                         // finding the point with maximum distance                   
                                         // from L and also on the specified side of L.                   
                                         for                               (                               int                               i=0; i<n; i++)                   
                                         {                   
                                         int                               temp = lineDist(p1, p2, a[i]);                   
                                         if                               (findSide(p1, p2, a[i]) == side && temp > max_dist)                   
                                         {                   
                                         ind = i;                   
                                         max_dist = temp;                   
                                         }                   
                                         }                   
                             
                                         // If no point is found, add the end points                   
                                         // of L to the convex hull.                   
                                         if                               (ind == -1)                   
                                         {                   
                                         hull.insert(p1);                   
                                         hull.insert(p2);                   
                                         return                               ;                   
                                         }                   
                             
                                         // Recur for the two parts divided by a[ind]                   
                                         quickHull(a, n, a[ind], p1, -findSide(a[ind], p1, p2));                   
                                         quickHull(a, n, a[ind], p2, -findSide(a[ind], p2, p1));                   
                     }                   
                             
                     void                               printHull(iPair a[],                               int                               n)                   
                     {                   
                                         // a[i].second -> y-coordinate of the ith point                   
                                         if                               (n < 3)                   
                                         {                   
                                         cout <<                               "Convex hull not possible"                               ;                   
                                         return                               ;                   
                                         }                   
                             
                                         // Finding the point with minimum and                   
                                         // maximum x-coordinate                   
                                         int                               min_x = 0, max_x = 0;                   
                                         for                               (                               int                               i=1; i<n; i++)                   
                                         {                   
                                         if                               (a[i].first < a[min_x].first)                   
                                         min_x = i;                   
                                         if                               (a[i].first > a[max_x].first)                   
                                         max_x = i;                   
                                         }                   
                             
                                         // Recursively find convex hull points on                   
                                         // one side of line joining a[min_x] and                   
                                         // a[max_x]                   
                                         quickHull(a, n, a[min_x], a[max_x], 1);                   
                             
                                         // Recursively find convex hull points on                   
                                         // other side of line joining a[min_x] and                   
                                         // a[max_x]                   
                                         quickHull(a, n, a[min_x], a[max_x], -1);                   
                             
                                         cout <<                               "The points in Convex Hull are:"                               ;                   
                                         while                               (!hull.empty())                   
                                         {                   
                                         cout <<                               "("                               <<( *hull.begin()).first <<                               ", "                   
                                         << (*hull.begin()).second <<                               ") "                               ;                   
                                         hull.erase(hull.begin());                   
                                         }                   
                     }                   
                             
                     // Driver code                   
                     int                               main()                   
                     {                   
                                         iPair a[] = {{0, 3}, {1, 1}, {2, 2}, {4, 4},                   
                                         {0, 0}, {1, 2}, {3, 1}, {3, 3}};                   
                                         int                               n =                               sizeof                               (a)/                               sizeof                               (a[0]);                   
                                         printHull(a, n);                   
                                         return                               0;                   
                     }                   

输入：

The points in Convex Hull are:
(0, 0) (0, 3) (3, 1) (4, 4)

时间复杂性： 该分析类似于快速排序。平均来说，我们得到的时间复杂度是O（n logn），但在最坏的情况下，它可能变成O（n） ^2. )

本文由 阿姆丽蒂娅·雅格尼 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用写极客。组织或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。

如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章