双端队列 是 队列数据结构 允许在两端插入和删除。在之前的帖子中,我们讨论了deque的介绍。现在在这篇文章中,我们将看到如何使用圆形数组实现deque。 Deque上的操作: 主要对队列执行以下四个基本操作: insertFront() :在Deque的前面添加一项。 insertRear() :在Deque的后面添加一项。 deleteFront() :从Deque前面删除一项。 deleteRear() :从Deque后面删除一项。 除上述操作外,还支持以下操作 getFront() :从队列中获取前面的项目。 getRear() :从队列中获取最后一项。 isEmpty() :检查Deque是否为空。 isFull() :检查Deque是否已满。
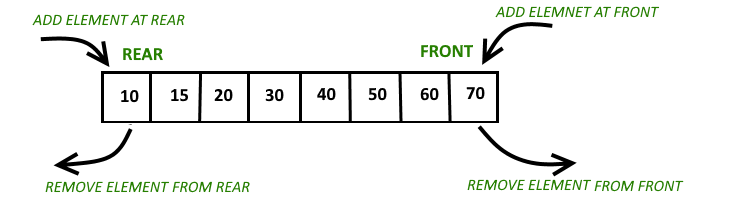
圆形阵列实现deque 为了实现deque,我们需要跟踪两个指标,前面和后面。我们在队列的后部或前端排队(推送)一件物品,并从后部和前部排队(弹出)一件物品。 工作 1.创建大小为“n”的空数组“arr” 初始化 正面=-1 , 后部=0 在deque中插入第一个元素,无论是在前面还是后面,都会得到相同的结果。
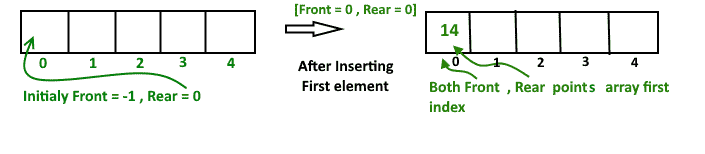
插入后 正面 分数=0和 后方的 分数=0 在后端插入元件
a). First we check deque if Full or Not
b). IF Rear == Size-1
then reinitialize Rear = 0 ;
Else increment Rear by '1'
and push current key into Arr[ rear ] = key
Front remain same.
在前端插入元件
a). First we check deque if Full or Not
b). IF Front == 0 || initial position, move Front
to points last index of array
front = size - 1
Else decremented front by '1' and push
current key into Arr[ Front] = key
Rear remain same.
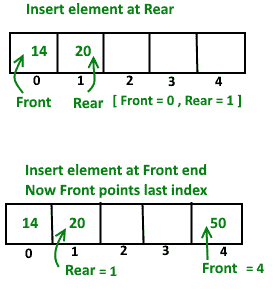
从后端删除元件
a). first Check deque is Empty or Not
b). If deque has only one element
front = -1 ; rear =-1 ;
Else IF Rear points to the first index of array
it's means we have to move rear to points
last index [ now first inserted element at
front end become rear end ]
rear = size-1 ;
Else || decrease rear by '1'
rear = rear-1;
从前端删除元素
a). first Check deque is Empty or Not
b). If deque has only one element
front = -1 ; rear =-1 ;
Else IF front points to the last index of the array
it's means we have no more elements in array so
we move front to points first index of array
front = 0 ;
Else || increment Front by '1'
front = front+1;
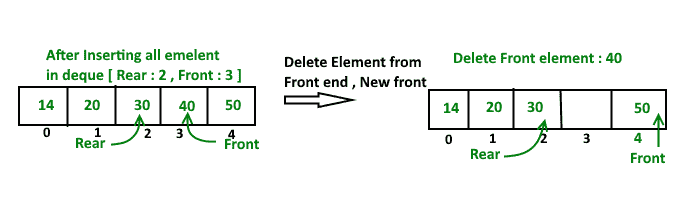
下面是上述想法的实现。
C++
// C++ implementation of De-queue using circular // array #include<iostream> using namespace std; // Maximum size of array or Dequeue #define MAX 100 // A structure to represent a Deque class Deque { int arr[MAX]; int front; int rear; int size; public : Deque( int size) { front = -1; rear = 0; this ->size = size; } // Operations on Deque: void insertfront( int key); void insertrear( int key); void deletefront(); void deleterear(); bool isFull(); bool isEmpty(); int getFront(); int getRear(); }; // Checks whether Deque is full or not. bool Deque::isFull() { return ((front == 0 && rear == size-1)|| front == rear+1); } // Checks whether Deque is empty or not. bool Deque::isEmpty () { return (front == -1); } // Inserts an element at front void Deque::insertfront( int key) { // check whether Deque if full or not if (isFull()) { cout << "Overflow" << endl; return ; } // If queue is initially empty if (front == -1) { front = 0; rear = 0; } // front is at first position of queue else if (front == 0) front = size - 1 ; else // decrement front end by '1' front = front-1; // insert current element into Deque arr[front] = key ; } // function to inset element at rear end // of Deque. void Deque ::insertrear( int key) { if (isFull()) { cout << " Overflow " << endl; return ; } // If queue is initially empty if (front == -1) { front = 0; rear = 0; } // rear is at last position of queue else if (rear == size-1) rear = 0; // increment rear end by '1' else rear = rear+1; // insert current element into Deque arr[rear] = key ; } // Deletes element at front end of Deque void Deque ::deletefront() { // check whether Deque is empty or not if (isEmpty()) { cout << "Queue Underflow" << endl; return ; } // Deque has only one element if (front == rear) { front = -1; rear = -1; } else // back to initial position if (front == size -1) front = 0; else // increment front by '1' to remove current // front value from Deque front = front+1; } // Delete element at rear end of Deque void Deque::deleterear() { if (isEmpty()) { cout << " Underflow" << endl ; return ; } // Deque has only one element if (front == rear) { front = -1; rear = -1; } else if (rear == 0) rear = size-1; else rear = rear-1; } // Returns front element of Deque int Deque::getFront() { // check whether Deque is empty or not if (isEmpty()) { cout << " Underflow" << endl; return -1 ; } return arr[front]; } // function return rear element of Deque int Deque::getRear() { // check whether Deque is empty or not if (isEmpty() || rear < 0) { cout << " Underflow" << endl; return -1 ; } return arr[rear]; } // Driver program to test above function int main() { Deque dq(5); cout << "Insert element at rear end : 5 " ; dq.insertrear(5); cout << "insert element at rear end : 10 " ; dq.insertrear(10); cout << "get rear element " << " " << dq.getRear() << endl; dq.deleterear(); cout << "After delete rear element new rear" << " become " << dq.getRear() << endl; cout << "inserting element at front end " ; dq.insertfront(15); cout << "get front element " << " " << dq.getFront() << endl; dq.deletefront(); cout << "After delete front element new " << "front become " << dq.getFront() << endl; return 0; } |
JAVA
// Java implementation of De-queue using circular // array // A structure to represent a Deque class Deque { static final int MAX = 100 ; int arr[]; int front; int rear; int size; public Deque( int size) { arr = new int [MAX]; front = - 1 ; rear = 0 ; this .size = size; } /*// Operations on Deque: void insertfront(int key); void insertrear(int key); void deletefront(); void deleterear(); bool isFull(); bool isEmpty(); int getFront(); int getRear();*/ // Checks whether Deque is full or not. boolean isFull() { return ((front == 0 && rear == size- 1 )|| front == rear+ 1 ); } // Checks whether Deque is empty or not. boolean isEmpty () { return (front == - 1 ); } // Inserts an element at front void insertfront( int key) { // check whether Deque if full or not if (isFull()) { System.out.println( "Overflow" ); return ; } // If queue is initially empty if (front == - 1 ) { front = 0 ; rear = 0 ; } // front is at first position of queue else if (front == 0 ) front = size - 1 ; else // decrement front end by '1' front = front- 1 ; // insert current element into Deque arr[front] = key ; } // function to inset element at rear end // of Deque. void insertrear( int key) { if (isFull()) { System.out.println( " Overflow " ); return ; } // If queue is initially empty if (front == - 1 ) { front = 0 ; rear = 0 ; } // rear is at last position of queue else if (rear == size- 1 ) rear = 0 ; // increment rear end by '1' else rear = rear+ 1 ; // insert current element into Deque arr[rear] = key ; } // Deletes element at front end of Deque void deletefront() { // check whether Deque is empty or not if (isEmpty()) { System.out.println( "Queue Underflow" ); return ; } // Deque has only one element if (front == rear) { front = - 1 ; rear = - 1 ; } else // back to initial position if (front == size - 1 ) front = 0 ; else // increment front by '1' to remove current // front value from Deque front = front+ 1 ; } // Delete element at rear end of Deque void deleterear() { if (isEmpty()) { System.out.println( " Underflow" ); return ; } // Deque has only one element if (front == rear) { front = - 1 ; rear = - 1 ; } else if (rear == 0 ) rear = size- 1 ; else rear = rear- 1 ; } // Returns front element of Deque int getFront() { // check whether Deque is empty or not if (isEmpty()) { System.out.println( " Underflow" ); return - 1 ; } return arr[front]; } // function return rear element of Deque int getRear() { // check whether Deque is empty or not if (isEmpty() || rear < 0 ) { System.out.println( " Underflow" ); return - 1 ; } return arr[rear]; } // Driver program to test above function public static void main(String[] args) { Deque dq = new Deque( 5 ); System.out.println( "Insert element at rear end : 5 " ); dq.insertrear( 5 ); System.out.println( "insert element at rear end : 10 " ); dq.insertrear( 10 ); System.out.println( "get rear element : " + dq.getRear()); dq.deleterear(); System.out.println( "After delete rear element new rear become : " + dq.getRear()); System.out.println( "inserting element at front end" ); dq.insertfront( 15 ); System.out.println( "get front element: " +dq.getFront()); dq.deletefront(); System.out.println( "After delete front element new front become : " + + dq.getFront()); } } |
Python3
# Python implementation of De-queue using circular # array # A structure to represent a Deque MAX = 100 ; class Deque: def __init__( self , size): self .arr = [ 0 ] * MAX self .front = - 1 ; self .rear = 0 ; self .size = size; ''' Operations on Deque: void insertfront(int key); void insertrear(int key); void deletefront(); void deleterear(); bool isFull(); bool isEmpty(); int getFront(); int getRear(); ''' # Checks whether Deque is full or not. def isFull( self ): return (( self .front = = 0 and self .rear = = self .size - 1 ) or self .front = = self .rear + 1 ) # Checks whether Deque is empty or not. def isEmpty ( self ): return ( self .front = = - 1 ); # Inserts an element at front def insertfront( self , key): # check whether Deque if full or not if ( self .isFull()): print ( "Overflow" ); return ; # If queue is initially empty if ( self .front = = - 1 ): self .front = 0 ; self .rear = 0 ; # front is at first position of queue elif ( self .front = = 0 ): self .front = self .size - 1 ; else : # decrement front end by '1' self .front = self .front - 1 ; # insert current element into Deque self .arr[ self .front] = key ; # function to inset element at rear end # of Deque. def insertrear( self , key): if ( self .isFull()): print ( " Overflow" ); return ; # If queue is initially empty if ( self .front = = - 1 ): self .front = 0 ; self .rear = 0 ; # rear is at last position of queue elif ( self .rear = = self .size - 1 ): self .rear = 0 ; # increment rear end by '1' else : self .rear = self .rear + 1 ; # insert current element into Deque self .arr[ self .rear] = key ; # Deletes element at front end of Deque def deletefront( self ): # check whether Deque is empty or not if ( self .isEmpty()): print ( "Queue Underflow" ); return ; # Deque has only one element if ( self .front = = self .rear): self .front = - 1 ; self .rear = - 1 ; else : # back to initial position if ( self .front = = self .size - 1 ): self .front = 0 ; else : # increment front by '1' to remove current # front value from Deque self .front = self .front + 1 ; # Delete element at rear end of Deque def deleterear( self ): if ( self .isEmpty()): print ( " Underflow" ); return ; # Deque has only one element if ( self .front = = self .rear): self .front = - 1 ; self .rear = - 1 ; elif ( self .rear = = 0 ): self .rear = self .size - 1 ; else : self .rear = self .rear - 1 ; # Returns front element of Deque def getFront( self ): # check whether Deque is empty or not if ( self .isEmpty()): print ( " Underflow" ); return - 1 ; return self .arr[ self .front]; # function return rear element of Deque def getRear( self ): # check whether Deque is empty or not if ( self .isEmpty() or self .rear < 0 ): print ( " Underflow" ); return - 1 ; return self .arr[ self .rear]; # Driver program to test above function dq = Deque( 5 ); print ( "Insert element at rear end : 5 " ); dq.insertrear( 5 ); print ( "insert element at rear end : 10 " ); dq.insertrear( 10 ); print (f "get rear element : {dq.getRear()}" ); dq.deleterear(); print (f "After delete rear element new rear become : {dq.getRear()}" ); print ( "inserting element at front end" ); dq.insertfront( 15 ); print (f "get front element: {dq.getFront()}" ); dq.deletefront(); print (f "After delete front element new front become : {dq.getFront()}" ); # This code is contributed by _saurabh_jaiswal |
C#
// C# implementation of De-queue using circular // array using System; // A structure to represent a Deque public class Deque { static readonly int MAX = 100; int []arr; int front; int rear; int size; public Deque( int size) { arr = new int [MAX]; front = -1; rear = 0; this .size = size; } /*// Operations on Deque: void insertfront(int key); void insertrear(int key); void deletefront(); void deleterear(); bool isFull(); bool .Count!=0; int getFront(); int getRear();*/ // Checks whether Deque is full or not. bool isFull() { return ((front == 0 && rear == size - 1)|| front == rear + 1); } // Checks whether Deque is empty or not. bool isEmpty () { return (front == -1); } // Inserts an element at front void insertfront( int key) { // check whether Deque if full or not if (isFull()) { Console.WriteLine( "Overflow" ); return ; } // If queue is initially empty if (front == -1) { front = 0; rear = 0; } // front is at first position of queue else if (front == 0) front = size - 1 ; else // decrement front end by '1' front = front - 1; // insert current element into Deque arr[front] = key ; } // function to inset element at rear end // of Deque. void insertrear( int key) { if (isFull()) { Console.WriteLine( " Overflow " ); return ; } // If queue is initially empty if (front == -1) { front = 0; rear = 0; } // rear is at last position of queue else if (rear == size - 1) rear = 0; // increment rear end by '1' else rear = rear+1; // insert current element into Deque arr[rear] = key ; } // Deletes element at front end of Deque void deletefront() { // check whether Deque is empty or not if (isEmpty()) { Console.WriteLine( "Queue Underflow" ); return ; } // Deque has only one element if (front == rear) { front = -1; rear = -1; } else // back to initial position if (front == size - 1) front = 0; else // increment front by '1' to remove current // front value from Deque front = front + 1; } // Delete element at rear end of Deque void deleterear() { if (isEmpty()) { Console.WriteLine( " Underflow" ); return ; } // Deque has only one element if (front == rear) { front = -1; rear = -1; } else if (rear == 0) rear = size - 1; else rear = rear - 1; } // Returns front element of Deque int getFront() { // check whether Deque is empty or not if (isEmpty()) { Console.WriteLine( " Underflow" ); return -1 ; } return arr[front]; } // function return rear element of Deque int getRear() { // check whether Deque is empty or not if (isEmpty() || rear < 0) { Console.WriteLine( " Underflow" ); return -1 ; } return arr[rear]; } // Driver code public static void Main(String[] args) { Deque dq = new Deque(5); Console.WriteLine( "Insert element at rear end : 5 " ); dq.insertrear(5); Console.WriteLine( "insert element at rear end : 10 " ); dq.insertrear(10); Console.WriteLine( "get rear element : " + dq.getRear()); dq.deleterear(); Console.WriteLine( "After delete rear element new rear become : " + dq.getRear()); Console.WriteLine( "inserting element at front end" ); dq.insertfront(15); Console.WriteLine( "get front element: " +dq.getFront()); dq.deletefront(); Console.WriteLine( "After delete front element new front become : " + + dq.getFront()); } } // This code is contributed by aashish1995 |
Javascript
<script> // Javascript implementation of De-queue using circular // array // A structure to represent a Deque let MAX = 100; class Deque { constructor(size) { this .arr = new Array(MAX); this .front = -1; this .rear = 0; this .size = size; } /*// Operations on Deque: void insertfront(int key); void insertrear(int key); void deletefront(); void deleterear(); bool isFull(); bool isEmpty(); int getFront(); int getRear();*/ // Checks whether Deque is full or not. isFull() { return (( this .front == 0 && this .rear == this .size-1)|| this .front == this .rear+1); } // Checks whether Deque is empty or not. isEmpty () { return ( this .front == -1); } // Inserts an element at front insertfront(key) { // check whether Deque if full or not if ( this .isFull()) { document.write( "Overflow<br>" ); return ; } // If queue is initially empty if ( this .front == -1) { this .front = 0; this .rear = 0; } // front is at first position of queue else if ( this .front == 0) this .front = this .size - 1 ; else // decrement front end by '1' this .front = this .front-1; // insert current element into Deque this .arr[ this .front] = key ; } // function to inset element at rear end // of Deque. insertrear(key) { if ( this .isFull()) { document.write( " Overflow <br>" ); return ; } // If queue is initially empty if ( this .front == -1) { this .front = 0; this .rear = 0; } // rear is at last position of queue else if ( this .rear == this .size-1) this .rear = 0; // increment rear end by '1' else this .rear = this .rear+1; // insert current element into Deque this .arr[ this .rear] = key ; } // Deletes element at front end of Deque deletefront() { // check whether Deque is empty or not if ( this .isEmpty()) { document.write( "Queue Underflow<br>" ); return ; } // Deque has only one element if ( this .front == this .rear) { this .front = -1; this .rear = -1; } else // back to initial position if ( this .front == this .size -1) this .front = 0; else // increment front by '1' to remove current // front value from Deque this .front = this .front+1; } // Delete element at rear end of Deque deleterear() { if ( this .isEmpty()) { document.write( " Underflow<br>" ); return ; } // Deque has only one element if ( this .front == this .rear) { this .front = -1; this .rear = -1; } else if ( this .rear == 0) this .rear = this .size-1; else this .rear = this .rear-1; } // Returns front element of Deque getFront() { // check whether Deque is empty or not if ( this .isEmpty()) { document.write( " Underflow<br>" ); return -1 ; } return this .arr[ this .front]; } // function return rear element of Deque getRear() { // check whether Deque is empty or not if ( this .isEmpty() || this .rear < 0) { document.write( " Underflow<br>" ); return -1 ; } return this .arr[ this .rear]; } } // Driver program to test above function let dq = new Deque(5); document.write( "Insert element at rear end : 5 <br>" ); dq.insertrear(5); document.write( "insert element at rear end : 10 <br>" ); dq.insertrear(10); document.write( "get rear element : " + dq.getRear()+ "<br>" ); dq.deleterear(); document.write( "After delete rear element new rear become : " + dq.getRear()+ "<br>" ); document.write( "inserting element at front end<br>" ); dq.insertfront(15); document.write( "get front element: " +dq.getFront()+ "<br>" ); dq.deletefront(); document.write( "After delete front element new front become : " + + dq.getFront()+ "<br>" ); // This code is contributed by avanitrachhadiya2155 </script> |
输出:
insert element at rear end : 5 insert element at rear end : 10 get rear element : 10 After delete rear element new rear become : 5 inserting element at front end get front element : 15 After delete front element new front become : 5
时间复杂度:insertfront()、insertlast()、deletefront()、deletelast()等所有操作的时间复杂度为O(1)。 在mext帖子中,我们将讨论使用双链表实现deque。 本文由 尼桑·辛格 .如果你喜欢GeekSforgek,并想贡献自己的力量,你也可以使用 写极客。组织 或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上,并帮助其他极客。 如果您发现任何不正确的地方,或者您想分享有关上述主题的更多信息,请写下评论。


![关于”PostgreSQL错误:关系[表]不存在“问题的原因和解决方案-yiteyi-C++库](https://www.yiteyi.com/wp-content/themes/zibll/img/thumbnail.svg)



