利用顶点离开时间的图的拓扑排序-yiteyi-C++库

给出一个有向无环图（DAG），求该图的拓扑排序。 拓扑排序 对于有向无环图（DAG），它是顶点的线性排序，因此对于每个有向边uv，顶点u在排序中位于v之前。如果图形不是DAG，则无法对其进行拓扑排序。例如，下图的拓扑排序为“5 4 2 3 1 0”。一个图可以有多个拓扑排序。例如，下图的另一个拓扑排序是“45 2 3 1 0”。

null

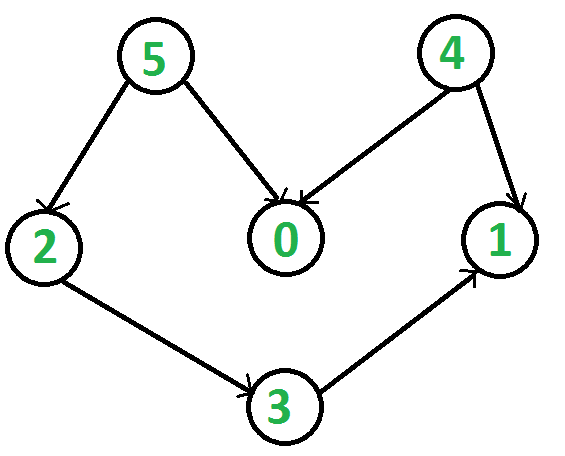
Topological Sort

请注意，拓扑排序中的第一个顶点始终是阶数为0的顶点（没有传入边的顶点）。对于上图，顶点4和5没有传入边。

推荐：请尝试你的方法 {IDE} 首先，在进入解决方案之前。

我们已经讨论了一个问题基于DFS的算法使用堆栈和卡恩算法用于拓扑排序。我们还讨论了如何打印各种拓扑结构的DAG 在这里 .在这篇文章中，通过引入 顶点到达和离开时间的概念 在DFS中。

DFS中顶点的到达时间和离开时间是多少？ 在DFS中， 到达时间 是第一次探索顶点的时间 出发时间 是我们已经探索了顶点的所有邻域并准备回溯的时间。

如何利用出发时间求图的拓扑排序？ 要找到拓扑类型的图，我们运行 DFS 从所有未访问的顶点逐个开始。对于任何一个顶点，在探索它的任何邻居之前，我们记录该顶点的到达时间，在探索该顶点的所有邻居之后，我们记录其离开时间。请注意，只需要离开时间就可以找到图的拓扑排序，所以我们可以跳过顶点的到达时间。最后，在我们访问了图中的所有顶点之后，我们按照它们离开时间的减少顺序打印这些顶点，这是我们想要的顶点拓扑顺序。以下是C++实现上述思想的方法——

C++

                         // A C++ program to print topological sorting of a DAG                       
                         #include <bits/stdc++.h>                       
                         using                                     namespace                                     std;                       
           
                         // Graph class represents a directed graph using adjacency                       
                         // list representation                       
                         class                                     Graph {                       
                                                 int                                     V;                                     // No. of vertices                       
                                                 // Pointer to an array containing adjacency lists                       
                                                 list<                                     int                                     >* adj;                       
           
                         public                                     :                       
                                                 Graph(                                     int                                     );                                     // Constructor                       
                                                 ~Graph();                                     // Destructor                       
           
                                                 // function to add an edge to graph                       
                                                 void                                     addEdge(                                     int                                     ,                                     int                                     );                       
           
                                                 // The function to do DFS traversal                       
                                                 void                                     DFS(                                     int                                     , vector<                                     bool                                     >&, vector<                                     int                                     >&,                                     int                                     &);                       
           
                                                 // The function to do Topological Sort.                       
                                                 void                                     topologicalSort();                       
                         };                       
           
                         Graph::Graph(                                     int                                     V)                       
                         {                       
                                                 this                                     ->V = V;                       
                                                 this                                     ->adj =                                     new                                     list<                                     int                                     >[V];                       
                         }                       
           
                         Graph::~Graph() {                                     delete                                     []                                     this                                     ->adj; }                       
           
                         void                                     Graph::addEdge(                                     int                                     v,                                     int                                     w)                       
                         {                       
                                                 adj[v].push_back(w);                                     // Add w to v's list.                       
                         }                       
           
                         // The function to do DFS() and stores departure time                       
                         // of all vertex                       
                         void                                     Graph::DFS(                                     int                                     v, vector<                                     bool                                     >& visited,                       
                                                 vector<                                     int                                     >& departure,                                     int                                     &                                     time                                     )                       
                         {                       
                                                 visited[v] =                                     true                                     ;                       
                                                 // time++;    // arrival time of vertex v                       
           
                                                 for                                     (                                     int                                     i : adj[v])                       
                                                 if                                     (!visited[i])                       
                                                 DFS(i, visited, departure,                                     time                                     );                       
           
                                                 // set departure time of vertex v                       
                                                 departure[                                     time                                     ++] = v;                       
                         }                       
           
                         // The function to do Topological Sort. It uses DFS().                       
                         void                                     Graph::topologicalSort()                       
                         {                       
                                                 // vector to store departure time of vertex.                       
                                                 vector<                                     int                                     > departure(V, -1);                       
           
                                                 // Mark all the vertices as not visited                       
                                                 vector<                                     bool                                     > visited(V,                                     false                                     );                       
                                                 int                                     time                                     = 0;                       
           
                                                 // perform DFS on all unvisited vertices                       
                                                 for                                     (                                     int                                     i = 0; i < V; i++) {                       
                                                 if                                     (visited[i] == 0) {                       
                                                 DFS(i, visited, departure,                                     time                                     );                       
                                                 }                       
                                                 }                       
                                                 // print the topological sort                       
                                                 for                                     (                                     int                                     i = V - 1; i >= 0; i--)                       
                                                 cout << departure[i] <<                                     " "                                     ;                       
                         }                       
           
                         // Driver program to test above functions                       
                         int                                     main()                       
                         {                       
                                                 // Create a graph given in the above diagram                       
                                                 Graph g(6);                       
                                                 g.addEdge(5, 2);                       
                                                 g.addEdge(5, 0);                       
                                                 g.addEdge(4, 0);                       
                                                 g.addEdge(4, 1);                       
                                                 g.addEdge(2, 3);                       
                                                 g.addEdge(3, 1);                       
           
                                                 cout <<                                     "Topological Sort of the given graph is "                                     ;                       
                                                 g.topologicalSort();                       
           
                                                 return                                     0;                       
                         }                       

Python3

                         # A Python3 program to print topological sorting of a DAG                       
                         def                                     addEdge(u, v):                       
                                                 global                                     adj                       
                                                 adj[u].append(v)                       
           
                         # The function to do DFS() and stores departure time                       
                         # of all vertex                       
                         def                                     DFS(v):                       
                                                 global                                     visited, departure, time                       
                                                 visited[v]                                     =                                     1                       
                                                 for                                     i                                     in                                     adj[v]:                       
                                                 if                                     visited[i]                                     =                                     =                                     0                                     :                       
                                                 DFS(i)                       
                                                 departure[time]                                     =                                     v                       
                                                 time                                     +                                     =                                     1                       
           
                         # The function to do Topological Sort. It uses DFS().                       
                         def                                     topologicalSort():                       
           
                                                 # perform DFS on all unvisited vertices                       
                                                 for                                     i                                     in                                     range                                     (V):                       
                                                 if                                     (visited[i]                                     =                                     =                                     0                                     ):                       
                                                 DFS(i)                       
           
                                                 # Print vertices in topological order                       
                                                 for                                     i                                     in                                     range                                     (V                                     -                                     1                                     ,                                     -                                     1                                     ,                                     -                                     1                                     ):                       
                                                 print                                     (departure[i], end                                     =                                     " "                                     )                       
           
                         # Driver code                       
                         if                                     __name__                                     =                                     =                                     '__main__'                                     :                       
                                   
                                                 # Create a graph given in the above diagram                       
                                                 V,time, adj, visited, departure                                     =                                     6                                     ,                                     0                                     , [[]                                     for                                     i                                     in                                     range                                     (                                     7                                     )], [                                     0                                     for                                     i                                     in                                     range                                     (                                     7                                     )],[                                     -                                     1                                     for                                     i                                     in                                     range                                     (                                     7                                     )]                       
                                                 addEdge(                                     5                                     ,                                     2                                     )                       
                                                 addEdge(                                     5                                     ,                                     0                                     )                       
                                                 addEdge(                                     4                                     ,                                     0                                     )                       
                                                 addEdge(                                     4                                     ,                                     1                                     )                       
                                                 addEdge(                                     2                                     ,                                     3                                     )                       
                                                 addEdge(                                     3                                     ,                                     1                                     )                       
           
                                                 print                                     (                                     "Topological Sort of the given graph is"                                     )                       
                                                 topologicalSort()                       
           
                         # This code is contributed by mohit kumar 29                       

Javascript

                         <script>                       
           
                         // A JavaScript program to print topological                       
                         // sorting of a DAG                       
                                   
                                                 let adj=                                     new                                     Array(7);                       
                                                 for                                     (let i=0;i<adj.length;i++)                       
                                                 {                       
                                                 adj[i]=[];                       
                                                 }                       
                                                 let V=6;                       
                                                 let time=0;                       
                                                 let visited=                                     new                                     Array(7);                       
                                                 let departure =                                     new                                     Array(7);                       
                                                 for                                     (let i=0;i<7;i++)                       
                                                 {                       
                                                 visited[i]=0;                       
                                                 departure[i]=-1;                       
                                                 }                       
                                                 function                                     addEdge(u, v)                       
                                                 {                       
                                                 adj[u].push(v)                       
                                                 }                       
                                   
                                                 // The function to do DFS() and                       
                                                 // stores departure time                       
                                                 // of all vertex                       
                                                 function                                     DFS(v)                       
                                                 {                       
                                                 visited[v] = 1;                       
                                                 for                                     (let i=0;i<adj[v].length;i++)                       
                                                 {                       
                                                 if                                     (visited[adj[v][i]]==0)                       
                                                 DFS(adj[v][i]);                       
                                                 }                       
                                                 departure[time] = v                       
                                                 time += 1                       
                                                 }                       
                                                 // The function to do Topological                       
                                                 // Sort. It uses DFS().                       
                                                 function                                     topologicalSort()                       
                                                 {                       
                                                 //perform DFS on all unvisited vertices                       
                                                 for                                     (let i=0;i<V;i++)                       
                                                 {                       
                                                 if                                     (visited[i] == 0)                       
                                                 DFS(i)                       
                                                 }                       
                                                 //perform DFS on all unvisited vertices                       
                                                 for                                     (let i=V-1;i>=0;i--)                       
                                                 {                       
                                                 document.write(departure[i]+                                     " "                                     );                       
                                                 }                       
                                                 }                       
                                   
                                                 // Create a graph given in the above diagram                       
                                   
                                                 addEdge(5, 2);                       
                                                 addEdge(5, 0);                       
                                                 addEdge(4, 0);                       
                                                 addEdge(4, 1);                       
                                                 addEdge(2, 3);                       
                                                 addEdge(3, 1);                       
                                                 document.write(                       
                                                 "Topological Sort of the given graph is<br>"                       
                                                 );                       
                                                 topologicalSort()                       
                                   
                                                 // This code is contributed by unknown2108                       
                                   
                         </script>                       

输出

Topological Sort of the given graph is 5 4 2 3 1 0

时间复杂性 上述溶液的浓度为O（V+E）。

本文由 阿迪蒂亚·戈尔 .如果你喜欢GeekSforgek，并想贡献自己的力量，你也可以使用写极客。组织或者把你的文章寄去评论-team@geeksforgeeks.org.看到你的文章出现在Geeksforgeks主页上，并帮助其他极客。如果您发现任何不正确的地方，或者您想分享有关上述主题的更多信息，请写下评论。

文章版权归作者所有，未经允许请勿转载。

THE END

技术文章